using CairoMakie
using Distributions

d = LogNormal(0, 2)
range_d = 0:0.001:4
q25 = quantile(d, 0.25)
q75 = quantile(d, 0.75)
credint = range(q25; stop=q75, length=100)
f, ax, l = lines(
    range_d,
    pdf.(d, range_d);
    linewidth=3,
    axis=(; limits=(-0.2, 4.2, nothing, nothing), xlabel=L"\theta", ylabel="Density"),
)
scatter!(ax, mode(d), pdf(d, mode(d)); color=:green, markersize=12)
band!(ax, credint, 0.0, pdf.(d, credint); color=(:steelblue, 0.5))
f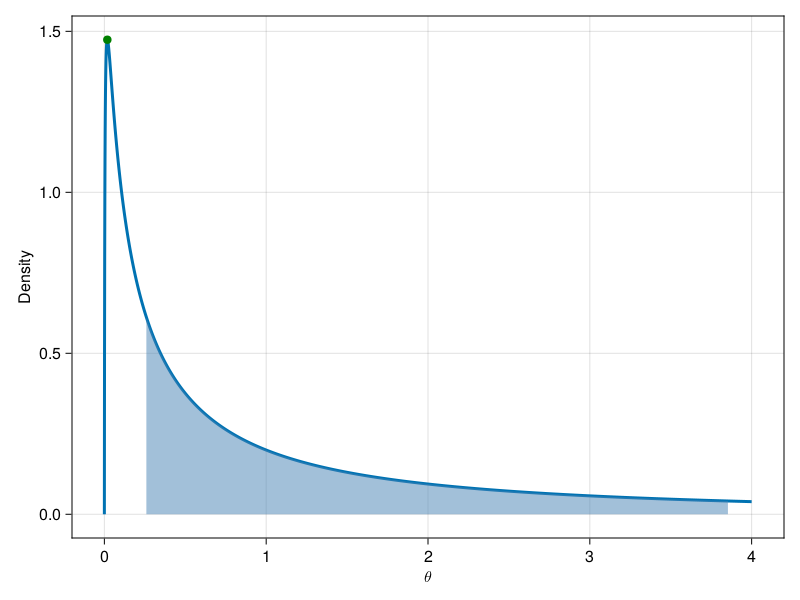

d1 = Normal(10, 1)
d2 = Normal(2, 1)
mix_d = [0.4, 0.6]
d = MixtureModel([d1, d2], mix_d)
range_d = -2:0.01:14
sim_d = rand(d, 10_000)
q25 = quantile(sim_d, 0.25)
q75 = quantile(sim_d, 0.75)
credint = range(q25; stop=q75, length=100)

f, ax, l = lines(
    range_d,
    pdf.(d, range_d);
    linewidth=3,
    axis=(;
        limits=(-2, 14, nothing, nothing),
        xticks=[0, 5, 10],
        xlabel=L"\theta",
        ylabel="Density",
    ),
)
scatter!(ax, mode(d2), pdf(d, mode(d2)); color=:green, markersize=12)
band!(ax, credint, 0.0, pdf.(d, credint); color=(:steelblue, 0.5))
f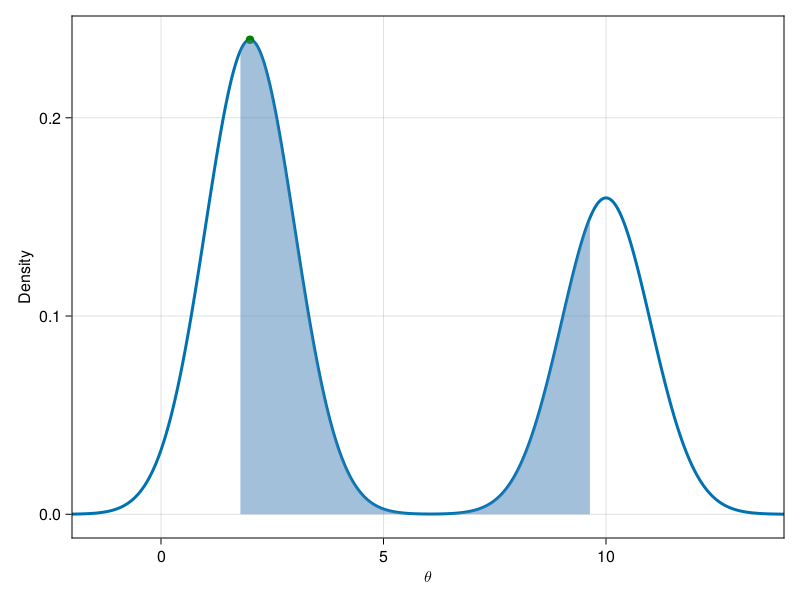

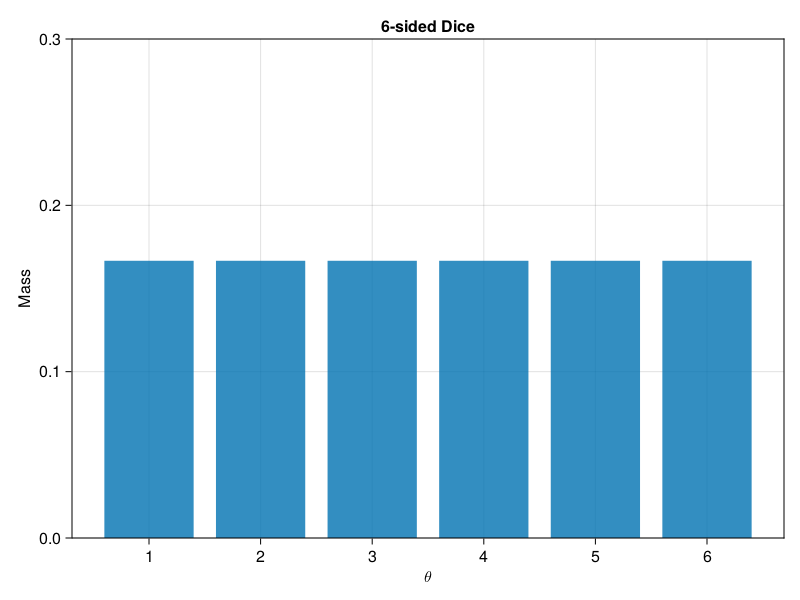
The discrete uniform

The discrete uniform distribution has two parameters and its notation is $Unif(a,b)$ - Lower Bound(a) - Upper Bound(b)

f, ax, b = barplot(
    DiscreteUniform(1, 6);
    axis=(;
        title="6-sided Dice",
        xlabel=L"\theta",
        ylabel="Mass",
        xticks=1:6,
        limits=(nothing, nothing, 0, 0.3),
    ),
)

Bernoulli

f, ax1, b = barplot(
    Bernoulli(0.5);
    width=0.3,
    axis=(;
        title=L"p=0.5",
        xlabel=L"\theta",
        ylabel="Mass",
        xticks=0:1,
        limits=(nothing, nothing, 0, 1)
    )
)
ax2 = Axis(
    f[1, 2]; title=L"p=0.2", xlabel=L"\theta", xticks=0:1, limits=(nothing, nothing, 0, 1)
)
barplot!(ax2, Bernoulli(0.2); width=0.3)
linkaxes!(ax1, ax2)

f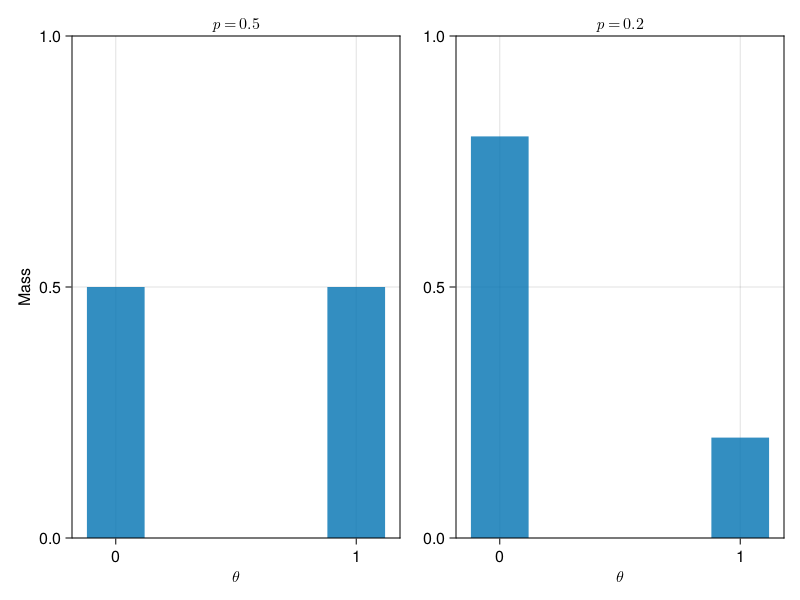

Binomial

The binomial distribution describes an event of the number of successes in a sequence of $n$ independent experiment(s), each asking a yes-no question with a probability

f, ax1, b = barplot(
    Binomial(5, 0.5); axis=(; title=L"p=0.5", xlabel=L"\theta", ylabel="Mass")
)
ax2 = Axis(f[1, 2]; title=L"p=0.2", xlabel=L"\theta")
barplot!(ax2, Binomial(5, 0.2))
linkaxes!(ax1, ax2)

Poisson

f, ax1, b = barplot(
    Poisson(1); axis=(; title=L"\lambda=1", xlabel=L"\theta", ylabel="Mass")
)
ax2 = Axis(f[1, 2]; title=L"\lambda=4", xlabel=L"\theta")
barplot!(ax2, Poisson(4))
linkaxes!(ax1, ax2)

How to use Turing

Turing is an ecosystem of Julia packages for Bayesian Inference using probabilistic programming. Turing provides an easy and intuitive way of specifying models.

Turing.jl is the main package in the Turing ecosystem and the backbone that glues all the other packages together. Turing’s “workflow” begin with a model specification. We specify the model inside a macro @model where we can assign variables in two ways:

• using ~: which means that a variable follows some probability distribution (Normal, Binomial etc.) and its value is random under that distribution
• using =: which means that a variable does not follow a probability distribution and its value is deterministic (like the normal = assignment in programming languages)

$$X\sim Uniform(1,6)$$ Note that the expectation of a random variable $X\sim Uniform(a,b)$ is $$E(X)=\frac{a+b}{2}=3.5$$

using CairoMakie
using Distributions

dice = DiscreteUniform(1, 6)
f, ax, b = barplot(
    dice;
    label="six-sided Dice",
    axis=(; xlabel=L"\theta", ylabel="Mass", xticks=1:6, limits=(nothing, nothing, 0, 0.3)),
)
vlines!(ax, [mean(dice)]; linewidth=5, color=:red, label=L"E(\theta)")
axislegend(ax)
f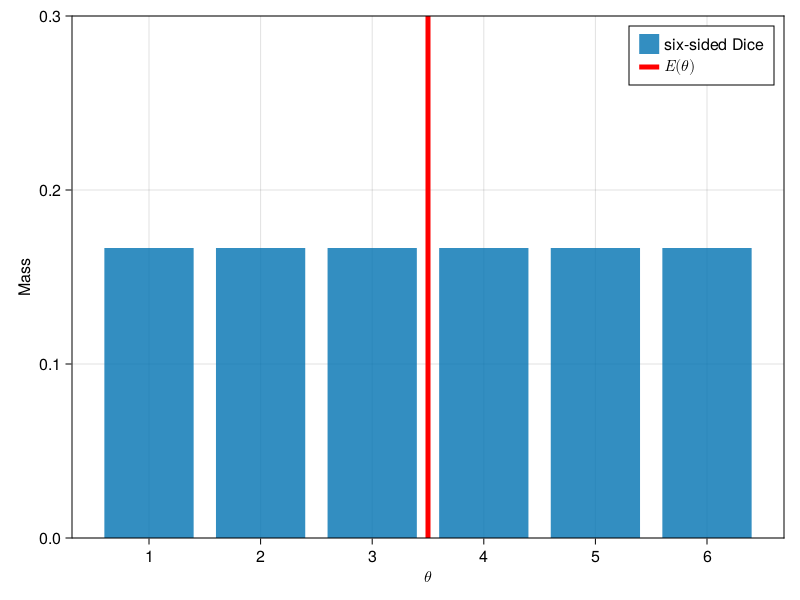

using Turing

@model function dice_throw(y)
    #Our prior belief about the probability of each result in a six-sided dice.
    #p is a vector of length 6 each with probability p that sums up to 1.
    p ~ Dirichlet(6, 1)

    #Each outcome of the six-sided dice has a probability p.
    for i in eachindex(y)
        y[i] ~ Categorical(p)
    end
end;

Dirichlet with a weekly informative prior towards a “fair” dice which is encoded as a Dirichlet(6,1)

mean(Dirichlet(6, 1))

6-element Fill{Float64}, with entries equal to 0.16666666666666666

sum(mean(Dirichlet(6, 1)))

1.0

using Random

Random.seed!(123);

my_data = rand(DiscreteUniform(1, 6), 1_000);

first(my_data, 10)

10-element Vector{Int64}:
 4
 4
 6
 2
 4
 3
 1
 6
 4
 2

@model function dice_throw(y)
    #Our prior belief about the probability of each result in a six-sided dice.
    #p is a vector of length 6 each with probability p that sums up to 1.
    p ~ Dirichlet(6, 1)

    #Each outcome of the six-sided dice has a probability p.
    for i in eachindex(y)
        y[i] ~ Categorical(p)
    end
end;

UndefVarError: UndefVarError: model not defined

Once the model is specified we instantiate the model with the single parameter y as the simulated my_data:

using MCMCChains

model = dice_throw(my_data);

chain = sample(model, NUTS(), 1_000);

Sampling   0%|                                          |  ETA: N/A

┌ Info: Found initial step size
│   ϵ = 0.2
└ @ Turing.Inference /Users/a182501/.julia/packages/Turing/Sj3CR/src/inference/hmc.jl:190
Sampling   0%|▎                                         |  ETA: 0:35:41

Sampling   1%|▍                                         |  ETA: 0:17:51
Sampling   1%|▋                                         |  ETA: 0:12:44

Sampling   2%|▊                                         |  ETA: 0:09:41

Sampling   2%|█                                         |  ETA: 0:07:56

Sampling   3%|█▏                                        |  ETA: 0:07:04

Sampling   3%|█▍                                        |  ETA: 0:06:24

Sampling   4%|█▋                                        |  ETA: 0:05:43

Sampling   4%|█▊                                        |  ETA: 0:05:18

Sampling   5%|██                                        |  ETA: 0:04:52

Sampling   5%|██▏                                       |  ETA: 0:04:39

Sampling   6%|██▍                                       |  ETA: 0:04:23

Sampling   6%|██▌                                       |  ETA: 0:04:10

Sampling   7%|██▊                                       |  ETA: 0:03:54

Sampling   7%|███                                       |  ETA: 0:03:56

Sampling   7%|███▏                                      |  ETA: 0:03:40
Sampling   8%|███▍                                      |  ETA: 0:03:29

Sampling   8%|███▌                                      |  ETA: 0:03:20

Sampling   9%|███▊                                      |  ETA: 0:03:11

Sampling   9%|███▉                                      |  ETA: 0:03:00
Sampling  10%|████▏                                     |  ETA: 0:02:54

Sampling  10%|████▎                                     |  ETA: 0:02:46

Sampling  11%|████▌                                     |  ETA: 0:02:42

Sampling  11%|████▊                                     |  ETA: 0:02:37

Sampling  12%|████▉                                     |  ETA: 0:02:35

Sampling  12%|█████▏                                    |  ETA: 0:02:34

Sampling  13%|█████▎                                    |  ETA: 0:02:30

Sampling  13%|█████▌                                    |  ETA: 0:02:25

Sampling  14%|█████▋                                    |  ETA: 0:02:23

Sampling  14%|█████▉                                    |  ETA: 0:02:21

Sampling  14%|██████▏                                   |  ETA: 0:02:16
Sampling  15%|██████▎                                   |  ETA: 0:02:11
Sampling  15%|██████▌                                   |  ETA: 0:02:08

Sampling  16%|██████▋                                   |  ETA: 0:02:09

Sampling  16%|██████▉                                   |  ETA: 0:02:07

Sampling  17%|███████                                   |  ETA: 0:02:04

Sampling  17%|███████▎                                  |  ETA: 0:02:00
Sampling  18%|███████▌                                  |  ETA: 0:01:56
Sampling  18%|███████▋                                  |  ETA: 0:01:54

Sampling  19%|███████▉                                  |  ETA: 0:01:53

Sampling  19%|████████                                  |  ETA: 0:01:51

Sampling  20%|████████▎                                 |  ETA: 0:01:48
Sampling  20%|████████▍                                 |  ETA: 0:01:48

Sampling  21%|████████▋                                 |  ETA: 0:01:47

Sampling  21%|████████▉                                 |  ETA: 0:01:45

Sampling  21%|█████████                                 |  ETA: 0:01:44

Sampling  22%|█████████▎                                |  ETA: 0:01:44

Sampling  22%|█████████▍                                |  ETA: 0:01:43

Sampling  23%|█████████▋                                |  ETA: 0:01:42

Sampling  23%|█████████▊                                |  ETA: 0:01:39
Sampling  24%|██████████                                |  ETA: 0:01:39

Sampling  24%|██████████▎                               |  ETA: 0:01:37

Sampling  25%|██████████▍                               |  ETA: 0:01:37

Sampling  25%|██████████▋                               |  ETA: 0:01:37

Sampling  26%|██████████▊                               |  ETA: 0:01:36

Sampling  26%|███████████                               |  ETA: 0:01:35

Sampling  27%|███████████▏                              |  ETA: 0:01:34

Sampling  27%|███████████▍                              |  ETA: 0:01:32

Sampling  28%|███████████▋                              |  ETA: 0:01:31

Sampling  28%|███████████▊                              |  ETA: 0:01:30

Sampling  28%|████████████                              |  ETA: 0:01:29

Sampling  29%|████████████▏                             |  ETA: 0:01:28

Sampling  29%|████████████▍                             |  ETA: 0:01:27

Sampling  30%|████████████▌                             |  ETA: 0:01:27

Sampling  30%|████████████▊                             |  ETA: 0:01:27

Sampling  31%|████████████▉                             |  ETA: 0:01:25

Sampling  31%|█████████████▏                            |  ETA: 0:01:25

Sampling  32%|█████████████▍                            |  ETA: 0:01:24

Sampling  32%|█████████████▌                            |  ETA: 0:01:23
Sampling  33%|█████████████▊                            |  ETA: 0:01:22

Sampling  33%|█████████████▉                            |  ETA: 0:01:21

Sampling  34%|██████████████▏                           |  ETA: 0:01:20

Sampling  34%|██████████████▎                           |  ETA: 0:01:19

Sampling  35%|██████████████▌                           |  ETA: 0:01:19

Sampling  35%|██████████████▊                           |  ETA: 0:01:19

Sampling  35%|██████████████▉                           |  ETA: 0:01:19

Sampling  36%|███████████████▏                          |  ETA: 0:01:18

Sampling  36%|███████████████▎                          |  ETA: 0:01:17

Sampling  37%|███████████████▌                          |  ETA: 0:01:16

Sampling  37%|███████████████▋                          |  ETA: 0:01:15

Sampling  38%|███████████████▉                          |  ETA: 0:01:14

Sampling  38%|████████████████▏                         |  ETA: 0:01:13

Sampling  39%|████████████████▎                         |  ETA: 0:01:12
Sampling  39%|████████████████▌                         |  ETA: 0:01:11

Sampling  40%|████████████████▋                         |  ETA: 0:01:10

Sampling  40%|████████████████▉                         |  ETA: 0:01:09

Sampling  41%|█████████████████                         |  ETA: 0:01:08

Sampling  41%|█████████████████▎                        |  ETA: 0:01:07

Sampling  42%|█████████████████▌                        |  ETA: 0:01:06
Sampling  42%|█████████████████▋                        |  ETA: 0:01:05

Sampling  42%|█████████████████▉                        |  ETA: 0:01:05

Sampling  43%|██████████████████                        |  ETA: 0:01:05

Sampling  43%|██████████████████▎                       |  ETA: 0:01:04

Sampling  44%|██████████████████▍                       |  ETA: 0:01:02
Sampling  44%|██████████████████▋                       |  ETA: 0:01:02

Sampling  45%|██████████████████▉                       |  ETA: 0:01:02

Sampling  45%|███████████████████                       |  ETA: 0:01:02

Sampling  46%|███████████████████▎                      |  ETA: 0:01:01

Sampling  46%|███████████████████▍                      |  ETA: 0:01:00
Sampling  47%|███████████████████▋                      |  ETA: 0:01:00

Sampling  47%|███████████████████▊                      |  ETA: 0:00:59

Sampling  48%|████████████████████                      |  ETA: 0:00:59

Sampling  48%|████████████████████▎                     |  ETA: 0:00:58

Sampling  49%|████████████████████▍                     |  ETA: 0:00:57

Sampling  49%|████████████████████▋                     |  ETA: 0:00:56
Sampling  49%|████████████████████▊                     |  ETA: 0:00:55
Sampling  50%|█████████████████████                     |  ETA: 0:00:55

Sampling  50%|█████████████████████▏                    |  ETA: 0:00:54

Sampling  51%|█████████████████████▍                    |  ETA: 0:00:54

Sampling  51%|█████████████████████▌                    |  ETA: 0:00:53

Sampling  52%|█████████████████████▊                    |  ETA: 0:00:52
Sampling  52%|██████████████████████                    |  ETA: 0:00:52

Sampling  53%|██████████████████████▏                   |  ETA: 0:00:51

Sampling  53%|██████████████████████▍                   |  ETA: 0:00:51

Sampling  54%|██████████████████████▌                   |  ETA: 0:00:50

Sampling  54%|██████████████████████▊                   |  ETA: 0:00:49

Sampling  55%|██████████████████████▉                   |  ETA: 0:00:49

Sampling  55%|███████████████████████▏                  |  ETA: 0:00:48

Sampling  56%|███████████████████████▍                  |  ETA: 0:00:48

Sampling  56%|███████████████████████▌                  |  ETA: 0:00:47

Sampling  56%|███████████████████████▊                  |  ETA: 0:00:47

Sampling  57%|███████████████████████▉                  |  ETA: 0:00:47

Sampling  57%|████████████████████████▏                 |  ETA: 0:00:46

Sampling  58%|████████████████████████▎                 |  ETA: 0:00:46

Sampling  58%|████████████████████████▌                 |  ETA: 0:00:45

Sampling  59%|████████████████████████▊                 |  ETA: 0:00:45

Sampling  59%|████████████████████████▉                 |  ETA: 0:00:45

Sampling  60%|█████████████████████████▏                |  ETA: 0:00:44

Sampling  60%|█████████████████████████▎                |  ETA: 0:00:43
Sampling  61%|█████████████████████████▌                |  ETA: 0:00:43

Sampling  61%|█████████████████████████▋                |  ETA: 0:00:42

Sampling  62%|█████████████████████████▉                |  ETA: 0:00:42
Sampling  62%|██████████████████████████▏               |  ETA: 0:00:41

Sampling  63%|██████████████████████████▎               |  ETA: 0:00:40

Sampling  63%|██████████████████████████▌               |  ETA: 0:00:40

Sampling  63%|██████████████████████████▋               |  ETA: 0:00:40

Sampling  64%|██████████████████████████▉               |  ETA: 0:00:39

Sampling  64%|███████████████████████████               |  ETA: 0:00:39

Sampling  65%|███████████████████████████▎              |  ETA: 0:00:39

Sampling  65%|███████████████████████████▌              |  ETA: 0:00:38

Sampling  66%|███████████████████████████▋              |  ETA: 0:00:38

Sampling  66%|███████████████████████████▉              |  ETA: 0:00:37

Sampling  67%|████████████████████████████              |  ETA: 0:00:37

Sampling  67%|████████████████████████████▎             |  ETA: 0:00:36
Sampling  68%|████████████████████████████▍             |  ETA: 0:00:36

Sampling  68%|████████████████████████████▋             |  ETA: 0:00:35

Sampling  69%|████████████████████████████▊             |  ETA: 0:00:34

Sampling  69%|█████████████████████████████             |  ETA: 0:00:34

Sampling  70%|█████████████████████████████▎            |  ETA: 0:00:33

Sampling  70%|█████████████████████████████▍            |  ETA: 0:00:33

Sampling  70%|█████████████████████████████▋            |  ETA: 0:00:32

Sampling  71%|█████████████████████████████▊            |  ETA: 0:00:32
Sampling  71%|██████████████████████████████            |  ETA: 0:00:31

Sampling  72%|██████████████████████████████▏           |  ETA: 0:00:31

Sampling  72%|██████████████████████████████▍           |  ETA: 0:00:30
Sampling  73%|██████████████████████████████▋           |  ETA: 0:00:29

Sampling  73%|██████████████████████████████▊           |  ETA: 0:00:29

Sampling  74%|███████████████████████████████           |  ETA: 0:00:29

Sampling  74%|███████████████████████████████▏          |  ETA: 0:00:28

Sampling  75%|███████████████████████████████▍          |  ETA: 0:00:28

Sampling  75%|███████████████████████████████▌          |  ETA: 0:00:27

Sampling  76%|███████████████████████████████▊          |  ETA: 0:00:27

Sampling  76%|████████████████████████████████          |  ETA: 0:00:26

Sampling  77%|████████████████████████████████▏         |  ETA: 0:00:25

Sampling  77%|████████████████████████████████▍         |  ETA: 0:00:25

Sampling  77%|████████████████████████████████▌         |  ETA: 0:00:24

Sampling  78%|████████████████████████████████▊         |  ETA: 0:00:24

Sampling  78%|████████████████████████████████▉         |  ETA: 0:00:23

Sampling  79%|█████████████████████████████████▏        |  ETA: 0:00:23
Sampling  79%|█████████████████████████████████▍        |  ETA: 0:00:22

Sampling  80%|█████████████████████████████████▌        |  ETA: 0:00:22

Sampling  80%|█████████████████████████████████▊        |  ETA: 0:00:21

Sampling  81%|█████████████████████████████████▉        |  ETA: 0:00:21

Sampling  81%|██████████████████████████████████▏       |  ETA: 0:00:20

Sampling  82%|██████████████████████████████████▎       |  ETA: 0:00:20

Sampling  82%|██████████████████████████████████▌       |  ETA: 0:00:19

Sampling  83%|██████████████████████████████████▊       |  ETA: 0:00:19

Sampling  83%|██████████████████████████████████▉       |  ETA: 0:00:18

Sampling  84%|███████████████████████████████████▏      |  ETA: 0:00:18

Sampling  84%|███████████████████████████████████▎      |  ETA: 0:00:17

Sampling  84%|███████████████████████████████████▌      |  ETA: 0:00:17

Sampling  85%|███████████████████████████████████▋      |  ETA: 0:00:16

Sampling  85%|███████████████████████████████████▉      |  ETA: 0:00:16

Sampling  86%|████████████████████████████████████▏     |  ETA: 0:00:15

Sampling  86%|████████████████████████████████████▎     |  ETA: 0:00:15

Sampling  87%|████████████████████████████████████▌     |  ETA: 0:00:14

Sampling  87%|████████████████████████████████████▋     |  ETA: 0:00:14

Sampling  88%|████████████████████████████████████▉     |  ETA: 0:00:13

Sampling  88%|█████████████████████████████████████     |  ETA: 0:00:13

Sampling  89%|█████████████████████████████████████▎    |  ETA: 0:00:12

Sampling  89%|█████████████████████████████████████▍    |  ETA: 0:00:12

Sampling  90%|█████████████████████████████████████▋    |  ETA: 0:00:11

Sampling  90%|█████████████████████████████████████▉    |  ETA: 0:00:11
Sampling  91%|██████████████████████████████████████    |  ETA: 0:00:10

Sampling  91%|██████████████████████████████████████▎   |  ETA: 0:00:10

Sampling  91%|██████████████████████████████████████▍   |  ETA: 0:00:09

Sampling  92%|██████████████████████████████████████▋   |  ETA: 0:00:09
Sampling  92%|██████████████████████████████████████▊   |  ETA: 0:00:08

Sampling  93%|███████████████████████████████████████   |  ETA: 0:00:08

Sampling  93%|███████████████████████████████████████▎  |  ETA: 0:00:07

Sampling  94%|███████████████████████████████████████▍  |  ETA: 0:00:07

Sampling  94%|███████████████████████████████████████▋  |  ETA: 0:00:06

Sampling  95%|███████████████████████████████████████▊  |  ETA: 0:00:06

Sampling  95%|████████████████████████████████████████  |  ETA: 0:00:05

Sampling  96%|████████████████████████████████████████▏ |  ETA: 0:00:05

Sampling  96%|████████████████████████████████████████▍ |  ETA: 0:00:04

Sampling  97%|████████████████████████████████████████▋ |  ETA: 0:00:04

Sampling  97%|████████████████████████████████████████▊ |  ETA: 0:00:03

Sampling  98%|█████████████████████████████████████████ |  ETA: 0:00:03

Sampling  98%|█████████████████████████████████████████▏|  ETA: 0:00:02

Sampling  98%|█████████████████████████████████████████▍|  ETA: 0:00:02

Sampling  99%|█████████████████████████████████████████▌|  ETA: 0:00:01

Sampling  99%|█████████████████████████████████████████▊|  ETA: 0:00:01

Sampling 100%|██████████████████████████████████████████|  ETA: 0:00:00

Sampling 100%|██████████████████████████████████████████| Time: 0:01:47

summaries, quantiles = describe(chain);

summaries

Summary Statistics
  parameters      mean       std      mcse    ess_bulk   ess_tail      rhat    ⋯
      Symbol   Float64   Float64   Float64     Float64    Float64   Float64    ⋯
        p[1]    0.1570    0.0112    0.0003   1555.2108   739.5350    1.0001    ⋯
        p[2]    0.1455    0.0110    0.0003   1368.0118   789.6229    1.0034    ⋯
        p[3]    0.1402    0.0114    0.0003   1418.4168   675.2338    0.9999    ⋯
        p[4]    0.1809    0.0118    0.0003   1922.1270   814.3606    0.9999    ⋯
        p[5]    0.1964    0.0128    0.0003   1543.1500   904.8074    1.0001    ⋯
        p[6]    0.1800    0.0118    0.0003   1331.7667   673.1075    0.9996    ⋯
                                                                1 column omitted

Here p is a 6-dimensional vector of probabilities, which each one associated with a mutually exclusive outcome of a six-sided dice throw. As we expected, the probabilities are almost equal to $\frac{1}{6}$

sum(summaries[:, :mean])

0.9999999999999998

sum([idx * i for (i, idx) in enumerate(summaries[:, :mean])])

3.6540660750844296

typeof(chain)

Chains{Float64, AxisArrays.AxisArray{Float64, 3, Array{Float64, 3}, Tuple{AxisArrays.Axis{:iter, StepRange{Int64, Int64}}, AxisArrays.Axis{:var, Vector{Symbol}}, AxisArrays.Axis{:chain, UnitRange{Int64}}}}, Missing, NamedTuple{(:parameters, :internals), Tuple{Vector{Symbol}, Vector{Symbol}}}, NamedTuple{(:start_time, :stop_time), Tuple{Float64, Float64}}}

using AlgebraOfGraphics
using AlgebraOfGraphics: density

┌ Warning: Module Tables with build ID 1429782626639209 is missing from the cache.
│ This may mean Tables [bd369af6-aec1-5ad0-b16a-f7cc5008161c] does not support precompilation but is imported by a module that does.
└ @ Base loading.jl:1325

┌ Warning: Module DataAPI with build ID 1429764053050668 is missing from the cache.
│ This may mean DataAPI [9a962f9c-6df0-11e9-0e5d-c546b8b5ee8a] does not support precompilation but is imported by a module that does.
└ @ Base loading.jl:1325

┌ Warning: Module Distributions with build ID 1540599512972250 is missing from the cache.
│ This may mean Distributions [31c24e10-a181-5473-b8eb-7969acd0382f] does not support precompilation but is imported by a module that does.
└ @ Base loading.jl:1325

┌ Warning: Module Tables with build ID 1429782626639209 is missing from the cache.
│ This may mean Tables [bd369af6-aec1-5ad0-b16a-f7cc5008161c] does not support precompilation but is imported by a module that does.
└ @ Base loading.jl:1325

params = names(chain, :parameters)
chain_mapping =
    mapping(params .=> "sample value") *
    mapping(; color=:chain => nonnumeric, row=dims(1) => renamer(params))
plt1 = data(chain) * mapping(:iteration) * chain_mapping * visual(Lines)
plt2 = data(chain) * chain_mapping * density()
f = Figure(; resolution=(800, 600))
draw!(f[1, 1], plt1)
draw!(f[1, 2], plt2; axis=(; ylabel="density"))

6×1 Matrix{AxisEntries}:
 AxisEntries(Axis (1 plots), Entry[Entry(Combined{AlgebraOfGraphics.linesfill}, Any[[0.09806009505544537, 0.09878869504166969, 0.099517295027894, 0.10024589501411832, 0.10097449500034264, 0.10170309498656695, 0.10243169497279127, 0.10316029495901559, 0.1038888949452399, 0.10461749493146422  …  0.2364940924380655, 0.2372226924242898, 0.23795129241051413, 0.23867989239673845, 0.23940849238296277, 0.2401370923691871, 0.2408656923554114, 0.2415942923416357, 0.24232289232786003, 0.24305149231408435], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0  …  0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]], {:color = RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), :cycle = nothing})], {:color = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.NonNumeric{Int64}}, Vector{ColorTypes.RGBA{Float32}}, Vector{ColorTypes.RGBA{Float32}}}(AlgebraOfGraphics.NonNumeric{Int64}[AlgebraOfGraphics.NonNumeric{Int64}(1)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), RGBA{Float32}(0.9019608f0,0.62352943f0,0.0f0,1.0f0), RGBA{Float32}(0.0f0,0.61960787f0,0.4509804f0,1.0f0), RGBA{Float32}(0.8f0,0.4745098f0,0.654902f0,1.0f0), RGBA{Float32}(0.3372549f0,0.7058824f0,0.9137255f0,1.0f0), RGBA{Float32}(0.8352941f0,0.36862746f0,0.0f0,1.0f0), RGBA{Float32}(0.9411765f0,0.89411765f0,0.25882354f0,1.0f0)], "chain"), :row = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.Sorted{Symbol}}, Base.OneTo{Int64}, MakieCore.Automatic}(AlgebraOfGraphics.Sorted{Symbol}[AlgebraOfGraphics.Sorted{Symbol}(0x00000001, Symbol("p[1]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000002, Symbol("p[2]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000003, Symbol("p[3]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000004, Symbol("p[4]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000005, Symbol("p[5]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000006, Symbol("p[6]"))], Base.OneTo(6), MakieCore.Automatic(), "")}, {1 = AlgebraOfGraphics.ContinuousScale{Float64}((0.09806009505544537, 0.24305149231408435), "sample value", false), 2 = AlgebraOfGraphics.ContinuousScale{Float64}((0.0, 34.73080119491376), "pdf", false)})
 AxisEntries(Axis (1 plots), Entry[Entry(Combined{AlgebraOfGraphics.linesfill}, Any[[0.09806009505544537, 0.09878869504166969, 0.099517295027894, 0.10024589501411832, 0.10097449500034264, 0.10170309498656695, 0.10243169497279127, 0.10316029495901559, 0.1038888949452399, 0.10461749493146422  …  0.2364940924380655, 0.2372226924242898, 0.23795129241051413, 0.23867989239673845, 0.23940849238296277, 0.2401370923691871, 0.2408656923554114, 0.2415942923416357, 0.24232289232786003, 0.24305149231408435], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.00010380605880241, 0.0001852368468670848  …  0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]], {:color = RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), :cycle = nothing})], {:color = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.NonNumeric{Int64}}, Vector{ColorTypes.RGBA{Float32}}, Vector{ColorTypes.RGBA{Float32}}}(AlgebraOfGraphics.NonNumeric{Int64}[AlgebraOfGraphics.NonNumeric{Int64}(1)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), RGBA{Float32}(0.9019608f0,0.62352943f0,0.0f0,1.0f0), RGBA{Float32}(0.0f0,0.61960787f0,0.4509804f0,1.0f0), RGBA{Float32}(0.8f0,0.4745098f0,0.654902f0,1.0f0), RGBA{Float32}(0.3372549f0,0.7058824f0,0.9137255f0,1.0f0), RGBA{Float32}(0.8352941f0,0.36862746f0,0.0f0,1.0f0), RGBA{Float32}(0.9411765f0,0.89411765f0,0.25882354f0,1.0f0)], "chain"), :row = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.Sorted{Symbol}}, Base.OneTo{Int64}, MakieCore.Automatic}(AlgebraOfGraphics.Sorted{Symbol}[AlgebraOfGraphics.Sorted{Symbol}(0x00000001, Symbol("p[1]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000002, Symbol("p[2]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000003, Symbol("p[3]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000004, Symbol("p[4]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000005, Symbol("p[5]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000006, Symbol("p[6]"))], Base.OneTo(6), MakieCore.Automatic(), "")}, {1 = AlgebraOfGraphics.ContinuousScale{Float64}((0.09806009505544537, 0.24305149231408435), "sample value", false), 2 = AlgebraOfGraphics.ContinuousScale{Float64}((0.0, 32.87023782312755), "pdf", false)})
 AxisEntries(Axis (1 plots), Entry[Entry(Combined{AlgebraOfGraphics.linesfill}, Any[[0.09806009505544537, 0.09878869504166969, 0.099517295027894, 0.10024589501411832, 0.10097449500034264, 0.10170309498656695, 0.10243169497279127, 0.10316029495901559, 0.1038888949452399, 0.10461749493146422  …  0.2364940924380655, 0.2372226924242898, 0.23795129241051413, 0.23867989239673845, 0.23940849238296277, 0.2401370923691871, 0.2408656923554114, 0.2415942923416357, 0.24232289232786003, 0.24305149231408435], [0.1544238536052144, 0.14849225386836779, 0.13205205898541805, 0.1089326477480937, 0.084179829548308, 0.06281053308367554, 0.04902459073258161, 0.04605243063436668, 0.05638777522588116, 0.08195883246382615  …  0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]], {:color = RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), :cycle = nothing})], {:color = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.NonNumeric{Int64}}, Vector{ColorTypes.RGBA{Float32}}, Vector{ColorTypes.RGBA{Float32}}}(AlgebraOfGraphics.NonNumeric{Int64}[AlgebraOfGraphics.NonNumeric{Int64}(1)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), RGBA{Float32}(0.9019608f0,0.62352943f0,0.0f0,1.0f0), RGBA{Float32}(0.0f0,0.61960787f0,0.4509804f0,1.0f0), RGBA{Float32}(0.8f0,0.4745098f0,0.654902f0,1.0f0), RGBA{Float32}(0.3372549f0,0.7058824f0,0.9137255f0,1.0f0), RGBA{Float32}(0.8352941f0,0.36862746f0,0.0f0,1.0f0), RGBA{Float32}(0.9411765f0,0.89411765f0,0.25882354f0,1.0f0)], "chain"), :row = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.Sorted{Symbol}}, Base.OneTo{Int64}, MakieCore.Automatic}(AlgebraOfGraphics.Sorted{Symbol}[AlgebraOfGraphics.Sorted{Symbol}(0x00000001, Symbol("p[1]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000002, Symbol("p[2]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000003, Symbol("p[3]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000004, Symbol("p[4]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000005, Symbol("p[5]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000006, Symbol("p[6]"))], Base.OneTo(6), MakieCore.Automatic(), "")}, {1 = AlgebraOfGraphics.ContinuousScale{Float64}((0.09806009505544537, 0.24305149231408435), "sample value", false), 2 = AlgebraOfGraphics.ContinuousScale{Float64}((0.0, 31.90119911044429), "pdf", false)})
 AxisEntries(Axis (1 plots), Entry[Entry(Combined{AlgebraOfGraphics.linesfill}, Any[[0.09806009505544537, 0.09878869504166969, 0.099517295027894, 0.10024589501411832, 0.10097449500034264, 0.10170309498656695, 0.10243169497279127, 0.10316029495901559, 0.1038888949452399, 0.10461749493146422  …  0.2364940924380655, 0.2372226924242898, 0.23795129241051413, 0.23867989239673845, 0.23940849238296277, 0.2401370923691871, 0.2408656923554114, 0.2415942923416357, 0.24232289232786003, 0.24305149231408435], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0  …  0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]], {:color = RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), :cycle = nothing})], {:color = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.NonNumeric{Int64}}, Vector{ColorTypes.RGBA{Float32}}, Vector{ColorTypes.RGBA{Float32}}}(AlgebraOfGraphics.NonNumeric{Int64}[AlgebraOfGraphics.NonNumeric{Int64}(1)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), RGBA{Float32}(0.9019608f0,0.62352943f0,0.0f0,1.0f0), RGBA{Float32}(0.0f0,0.61960787f0,0.4509804f0,1.0f0), RGBA{Float32}(0.8f0,0.4745098f0,0.654902f0,1.0f0), RGBA{Float32}(0.3372549f0,0.7058824f0,0.9137255f0,1.0f0), RGBA{Float32}(0.8352941f0,0.36862746f0,0.0f0,1.0f0), RGBA{Float32}(0.9411765f0,0.89411765f0,0.25882354f0,1.0f0)], "chain"), :row = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.Sorted{Symbol}}, Base.OneTo{Int64}, MakieCore.Automatic}(AlgebraOfGraphics.Sorted{Symbol}[AlgebraOfGraphics.Sorted{Symbol}(0x00000001, Symbol("p[1]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000002, Symbol("p[2]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000003, Symbol("p[3]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000004, Symbol("p[4]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000005, Symbol("p[5]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000006, Symbol("p[6]"))], Base.OneTo(6), MakieCore.Automatic(), "")}, {1 = AlgebraOfGraphics.ContinuousScale{Float64}((0.09806009505544537, 0.24305149231408435), "sample value", false), 2 = AlgebraOfGraphics.ContinuousScale{Float64}((0.0, 32.88029194970536), "pdf", false)})
 AxisEntries(Axis (1 plots), Entry[Entry(Combined{AlgebraOfGraphics.linesfill}, Any[[0.09806009505544537, 0.09878869504166969, 0.099517295027894, 0.10024589501411832, 0.10097449500034264, 0.10170309498656695, 0.10243169497279127, 0.10316029495901559, 0.1038888949452399, 0.10461749493146422  …  0.2364940924380655, 0.2372226924242898, 0.23795129241051413, 0.23867989239673845, 0.23940849238296277, 0.2401370923691871, 0.2408656923554114, 0.2415942923416357, 0.24232289232786003, 0.24305149231408435], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0  …  0.23540815399158949, 0.1710554882427096, 0.12745636133159735, 0.10366920151741194, 0.09677913264728924, 0.10236413297269305, 0.11505919958710743, 0.12924937868259612, 0.13989519699809116, 0.14336976289796938]], {:color = RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), :cycle = nothing})], {:color = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.NonNumeric{Int64}}, Vector{ColorTypes.RGBA{Float32}}, Vector{ColorTypes.RGBA{Float32}}}(AlgebraOfGraphics.NonNumeric{Int64}[AlgebraOfGraphics.NonNumeric{Int64}(1)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), RGBA{Float32}(0.9019608f0,0.62352943f0,0.0f0,1.0f0), RGBA{Float32}(0.0f0,0.61960787f0,0.4509804f0,1.0f0), RGBA{Float32}(0.8f0,0.4745098f0,0.654902f0,1.0f0), RGBA{Float32}(0.3372549f0,0.7058824f0,0.9137255f0,1.0f0), RGBA{Float32}(0.8352941f0,0.36862746f0,0.0f0,1.0f0), RGBA{Float32}(0.9411765f0,0.89411765f0,0.25882354f0,1.0f0)], "chain"), :row = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.Sorted{Symbol}}, Base.OneTo{Int64}, MakieCore.Automatic}(AlgebraOfGraphics.Sorted{Symbol}[AlgebraOfGraphics.Sorted{Symbol}(0x00000001, Symbol("p[1]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000002, Symbol("p[2]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000003, Symbol("p[3]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000004, Symbol("p[4]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000005, Symbol("p[5]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000006, Symbol("p[6]"))], Base.OneTo(6), MakieCore.Automatic(), "")}, {1 = AlgebraOfGraphics.ContinuousScale{Float64}((0.09806009505544537, 0.24305149231408435), "sample value", false), 2 = AlgebraOfGraphics.ContinuousScale{Float64}((0.0, 32.277620313021764), "pdf", false)})
 AxisEntries(Axis (1 plots), Entry[Entry(Combined{AlgebraOfGraphics.linesfill}, Any[[0.09806009505544537, 0.09878869504166969, 0.099517295027894, 0.10024589501411832, 0.10097449500034264, 0.10170309498656695, 0.10243169497279127, 0.10316029495901559, 0.1038888949452399, 0.10461749493146422  …  0.2364940924380655, 0.2372226924242898, 0.23795129241051413, 0.23867989239673845, 0.23940849238296277, 0.2401370923691871, 0.2408656923554114, 0.2415942923416357, 0.24232289232786003, 0.24305149231408435], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0  …  0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]], {:color = RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), :cycle = nothing})], {:color = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.NonNumeric{Int64}}, Vector{ColorTypes.RGBA{Float32}}, Vector{ColorTypes.RGBA{Float32}}}(AlgebraOfGraphics.NonNumeric{Int64}[AlgebraOfGraphics.NonNumeric{Int64}(1)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0)], ColorTypes.RGBA{Float32}[RGBA{Float32}(0.0f0,0.44705883f0,0.69803923f0,1.0f0), RGBA{Float32}(0.9019608f0,0.62352943f0,0.0f0,1.0f0), RGBA{Float32}(0.0f0,0.61960787f0,0.4509804f0,1.0f0), RGBA{Float32}(0.8f0,0.4745098f0,0.654902f0,1.0f0), RGBA{Float32}(0.3372549f0,0.7058824f0,0.9137255f0,1.0f0), RGBA{Float32}(0.8352941f0,0.36862746f0,0.0f0,1.0f0), RGBA{Float32}(0.9411765f0,0.89411765f0,0.25882354f0,1.0f0)], "chain"), :row = AlgebraOfGraphics.CategoricalScale{Vector{AlgebraOfGraphics.Sorted{Symbol}}, Base.OneTo{Int64}, MakieCore.Automatic}(AlgebraOfGraphics.Sorted{Symbol}[AlgebraOfGraphics.Sorted{Symbol}(0x00000001, Symbol("p[1]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000002, Symbol("p[2]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000003, Symbol("p[3]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000004, Symbol("p[4]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000005, Symbol("p[5]")), AlgebraOfGraphics.Sorted{Symbol}(0x00000006, Symbol("p[6]"))], Base.OneTo(6), MakieCore.Automatic(), "")}, {1 = AlgebraOfGraphics.ContinuousScale{Float64}((0.09806009505544537, 0.24305149231408435), "sample value", false), 2 = AlgebraOfGraphics.ContinuousScale{Float64}((0.0, 31.156345236700602), "pdf", false)})

f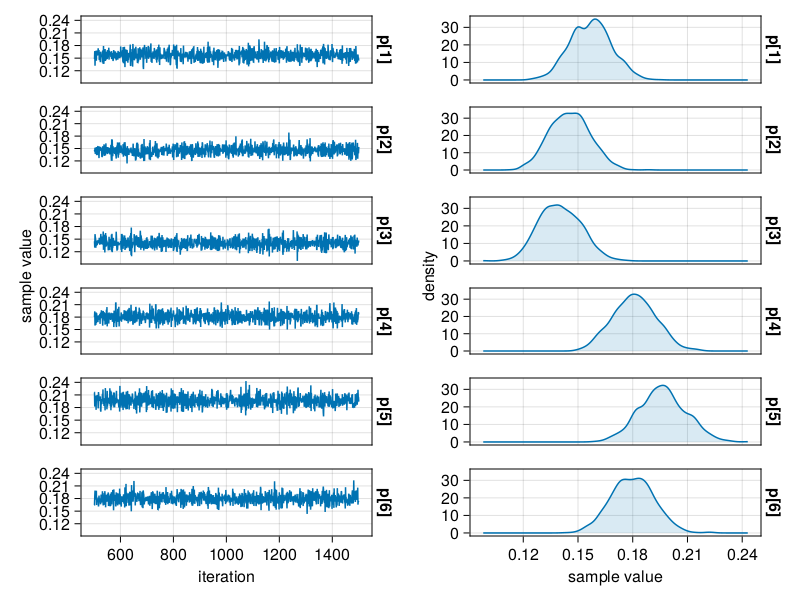

On the figure above we can see, for each parameter in the model, on the left the parameter’s traceplot and on the right the parameter’s density.

Prior and Posterior Predictive Checks

Predictive checks are a great way to validate a model. The idea is to generate data from the model using parameters from draws from the prior or posterior. Prior predictive check is when we simulate data using model parameter values drawn fom the prior distribution, and posterior predictive check is is when we simulate data using model parameter values drawn fom the posterior distribution.

prior_chain = sample(model, Prior(), 2_000);

Sampling   0%|                                          |  ETA: N/A

Sampling   0%|▎                                         |  ETA: 0:00:28
Sampling   1%|▍                                         |  ETA: 0:00:14
Sampling   2%|▋                                         |  ETA: 0:00:09
Sampling   2%|▉                                         |  ETA: 0:00:07
Sampling   2%|█                                         |  ETA: 0:00:06
Sampling   3%|█▎                                        |  ETA: 0:00:05
Sampling   4%|█▌                                        |  ETA: 0:00:04
Sampling   4%|█▋                                        |  ETA: 0:00:04
Sampling   4%|█▉                                        |  ETA: 0:00:03
Sampling   5%|██▏                                       |  ETA: 0:00:03
Sampling   6%|██▎                                       |  ETA: 0:00:03
Sampling   6%|██▌                                       |  ETA: 0:00:03
Sampling   6%|██▊                                       |  ETA: 0:00:02
Sampling   7%|███                                       |  ETA: 0:00:02
Sampling   8%|███▏                                      |  ETA: 0:00:02
Sampling   8%|███▍                                      |  ETA: 0:00:02
Sampling   8%|███▋                                      |  ETA: 0:00:02
Sampling   9%|███▊                                      |  ETA: 0:00:02
Sampling  10%|████                                      |  ETA: 0:00:02
Sampling  10%|████▎                                     |  ETA: 0:00:02
Sampling  10%|████▍                                     |  ETA: 0:00:02
Sampling  11%|████▋                                     |  ETA: 0:00:01
Sampling  12%|████▉                                     |  ETA: 0:00:01
Sampling  12%|█████                                     |  ETA: 0:00:01
Sampling  12%|█████▎                                    |  ETA: 0:00:01
Sampling  13%|█████▌                                    |  ETA: 0:00:01
Sampling  14%|█████▋                                    |  ETA: 0:00:01
Sampling  14%|█████▉                                    |  ETA: 0:00:01
Sampling  14%|██████▏                                   |  ETA: 0:00:01
Sampling  15%|██████▎                                   |  ETA: 0:00:01
Sampling  16%|██████▌                                   |  ETA: 0:00:01
Sampling  16%|██████▊                                   |  ETA: 0:00:01
Sampling  16%|██████▉                                   |  ETA: 0:00:01
Sampling  17%|███████▏                                  |  ETA: 0:00:01
Sampling  18%|███████▍                                  |  ETA: 0:00:01
Sampling  18%|███████▌                                  |  ETA: 0:00:01
Sampling  18%|███████▊                                  |  ETA: 0:00:01
Sampling  19%|████████                                  |  ETA: 0:00:01
Sampling  20%|████████▎                                 |  ETA: 0:00:01
Sampling  20%|████████▍                                 |  ETA: 0:00:01
Sampling  20%|████████▋                                 |  ETA: 0:00:01
Sampling  21%|████████▉                                 |  ETA: 0:00:01
Sampling  22%|█████████                                 |  ETA: 0:00:01
Sampling  22%|█████████▎                                |  ETA: 0:00:01

Sampling  22%|█████████▌                                |  ETA: 0:00:01
Sampling  23%|█████████▋                                |  ETA: 0:00:01
Sampling  24%|█████████▉                                |  ETA: 0:00:01
Sampling  24%|██████████▏                               |  ETA: 0:00:01
Sampling  24%|██████████▎                               |  ETA: 0:00:01
Sampling  25%|██████████▌                               |  ETA: 0:00:01
Sampling  26%|██████████▊                               |  ETA: 0:00:01
Sampling  26%|██████████▉                               |  ETA: 0:00:01
Sampling  26%|███████████▏                              |  ETA: 0:00:01
Sampling  27%|███████████▍                              |  ETA: 0:00:01
Sampling  28%|███████████▌                              |  ETA: 0:00:01
Sampling  28%|███████████▊                              |  ETA: 0:00:01
Sampling  28%|████████████                              |  ETA: 0:00:01
Sampling  29%|████████████▏                             |  ETA: 0:00:01
Sampling  30%|████████████▍                             |  ETA: 0:00:01
Sampling  30%|████████████▋                             |  ETA: 0:00:01
Sampling  30%|████████████▊                             |  ETA: 0:00:01
Sampling  31%|█████████████                             |  ETA: 0:00:01
Sampling  32%|█████████████▎                            |  ETA: 0:00:01
Sampling  32%|█████████████▌                            |  ETA: 0:00:01
Sampling  32%|█████████████▋                            |  ETA: 0:00:01
Sampling  33%|█████████████▉                            |  ETA: 0:00:01
Sampling  34%|██████████████▏                           |  ETA: 0:00:01
Sampling  34%|██████████████▎                           |  ETA: 0:00:01
Sampling  34%|██████████████▌                           |  ETA: 0:00:01
Sampling  35%|██████████████▊                           |  ETA: 0:00:01
Sampling  36%|██████████████▉                           |  ETA: 0:00:01
Sampling  36%|███████████████▏                          |  ETA: 0:00:01
Sampling  36%|███████████████▍                          |  ETA: 0:00:01
Sampling  37%|███████████████▌                          |  ETA: 0:00:01
Sampling  38%|███████████████▊                          |  ETA: 0:00:01
Sampling  38%|████████████████                          |  ETA: 0:00:01
Sampling  38%|████████████████▏                         |  ETA: 0:00:01

Sampling  39%|████████████████▍                         |  ETA: 0:00:01
Sampling  40%|████████████████▋                         |  ETA: 0:00:01
Sampling  40%|████████████████▊                         |  ETA: 0:00:01
Sampling  40%|█████████████████                         |  ETA: 0:00:01
Sampling  41%|█████████████████▎                        |  ETA: 0:00:01
Sampling  42%|█████████████████▍                        |  ETA: 0:00:01
Sampling  42%|█████████████████▋                        |  ETA: 0:00:00
Sampling  42%|█████████████████▉                        |  ETA: 0:00:00
Sampling  43%|██████████████████                        |  ETA: 0:00:00
Sampling  44%|██████████████████▎                       |  ETA: 0:00:00
Sampling  44%|██████████████████▌                       |  ETA: 0:00:00
Sampling  44%|██████████████████▊                       |  ETA: 0:00:00
Sampling  45%|██████████████████▉                       |  ETA: 0:00:00
Sampling  46%|███████████████████▏                      |  ETA: 0:00:00
Sampling  46%|███████████████████▍                      |  ETA: 0:00:00
Sampling  46%|███████████████████▌                      |  ETA: 0:00:00
Sampling  47%|███████████████████▊                      |  ETA: 0:00:00
Sampling  48%|████████████████████                      |  ETA: 0:00:00
Sampling  48%|████████████████████▏                     |  ETA: 0:00:00
Sampling  48%|████████████████████▍                     |  ETA: 0:00:00
Sampling  49%|████████████████████▋                     |  ETA: 0:00:00
Sampling  50%|████████████████████▊                     |  ETA: 0:00:00
Sampling  50%|█████████████████████                     |  ETA: 0:00:00
Sampling  50%|█████████████████████▎                    |  ETA: 0:00:00
Sampling  51%|█████████████████████▍                    |  ETA: 0:00:00
Sampling  52%|█████████████████████▋                    |  ETA: 0:00:00
Sampling  52%|█████████████████████▉                    |  ETA: 0:00:00
Sampling  52%|██████████████████████                    |  ETA: 0:00:00
Sampling  53%|██████████████████████▎                   |  ETA: 0:00:00
Sampling  54%|██████████████████████▌                   |  ETA: 0:00:00
Sampling  54%|██████████████████████▋                   |  ETA: 0:00:00
Sampling  55%|██████████████████████▉                   |  ETA: 0:00:00
Sampling  55%|███████████████████████▏                  |  ETA: 0:00:00
Sampling  56%|███████████████████████▎                  |  ETA: 0:00:00
Sampling  56%|███████████████████████▌                  |  ETA: 0:00:00

Sampling  56%|███████████████████████▊                  |  ETA: 0:00:00
Sampling  57%|████████████████████████                  |  ETA: 0:00:00
Sampling  57%|████████████████████████▏                 |  ETA: 0:00:00
Sampling  58%|████████████████████████▍                 |  ETA: 0:00:00
Sampling  58%|████████████████████████▋                 |  ETA: 0:00:00
Sampling  59%|████████████████████████▊                 |  ETA: 0:00:00
Sampling  60%|█████████████████████████                 |  ETA: 0:00:00
Sampling  60%|█████████████████████████▎                |  ETA: 0:00:00
Sampling  60%|█████████████████████████▍                |  ETA: 0:00:00
Sampling  61%|█████████████████████████▋                |  ETA: 0:00:00
Sampling  62%|█████████████████████████▉                |  ETA: 0:00:00
Sampling  62%|██████████████████████████                |  ETA: 0:00:00

Sampling  62%|██████████████████████████▎               |  ETA: 0:00:00
Sampling  63%|██████████████████████████▌               |  ETA: 0:00:00
Sampling  64%|██████████████████████████▋               |  ETA: 0:00:00
Sampling  64%|██████████████████████████▉               |  ETA: 0:00:00
Sampling  64%|███████████████████████████▏              |  ETA: 0:00:00
Sampling  65%|███████████████████████████▎              |  ETA: 0:00:00
Sampling  66%|███████████████████████████▌              |  ETA: 0:00:00
Sampling  66%|███████████████████████████▊              |  ETA: 0:00:00
Sampling  66%|███████████████████████████▉              |  ETA: 0:00:00
Sampling  67%|████████████████████████████▏             |  ETA: 0:00:00
Sampling  68%|████████████████████████████▍             |  ETA: 0:00:00
Sampling  68%|████████████████████████████▌             |  ETA: 0:00:00
Sampling  68%|████████████████████████████▊             |  ETA: 0:00:00
Sampling  69%|█████████████████████████████             |  ETA: 0:00:00
Sampling  70%|█████████████████████████████▎            |  ETA: 0:00:00
Sampling  70%|█████████████████████████████▍            |  ETA: 0:00:00
Sampling  70%|█████████████████████████████▋            |  ETA: 0:00:00
Sampling  71%|█████████████████████████████▉            |  ETA: 0:00:00
Sampling  72%|██████████████████████████████            |  ETA: 0:00:00
Sampling  72%|██████████████████████████████▎           |  ETA: 0:00:00
Sampling  72%|██████████████████████████████▌           |  ETA: 0:00:00
Sampling  73%|██████████████████████████████▋           |  ETA: 0:00:00
Sampling  74%|██████████████████████████████▉           |  ETA: 0:00:00
Sampling  74%|███████████████████████████████▏          |  ETA: 0:00:00
Sampling  74%|███████████████████████████████▎          |  ETA: 0:00:00
Sampling  75%|███████████████████████████████▌          |  ETA: 0:00:00
Sampling  76%|███████████████████████████████▊          |  ETA: 0:00:00
Sampling  76%|███████████████████████████████▉          |  ETA: 0:00:00
Sampling  76%|████████████████████████████████▏         |  ETA: 0:00:00
Sampling  77%|████████████████████████████████▍         |  ETA: 0:00:00
Sampling  78%|████████████████████████████████▌         |  ETA: 0:00:00
Sampling  78%|████████████████████████████████▊         |  ETA: 0:00:00
Sampling  78%|█████████████████████████████████         |  ETA: 0:00:00
Sampling  79%|█████████████████████████████████▏        |  ETA: 0:00:00
Sampling  80%|█████████████████████████████████▍        |  ETA: 0:00:00
Sampling  80%|█████████████████████████████████▋        |  ETA: 0:00:00
Sampling  80%|█████████████████████████████████▊        |  ETA: 0:00:00
Sampling  81%|██████████████████████████████████        |  ETA: 0:00:00
Sampling  82%|██████████████████████████████████▎       |  ETA: 0:00:00
Sampling  82%|██████████████████████████████████▌       |  ETA: 0:00:00
Sampling  82%|██████████████████████████████████▋       |  ETA: 0:00:00
Sampling  83%|██████████████████████████████████▉       |  ETA: 0:00:00
Sampling  84%|███████████████████████████████████▏      |  ETA: 0:00:00
Sampling  84%|███████████████████████████████████▎      |  ETA: 0:00:00
Sampling  84%|███████████████████████████████████▌      |  ETA: 0:00:00
Sampling  85%|███████████████████████████████████▊      |  ETA: 0:00:00
Sampling  86%|███████████████████████████████████▉      |  ETA: 0:00:00
Sampling  86%|████████████████████████████████████▏     |  ETA: 0:00:00
Sampling  86%|████████████████████████████████████▍     |  ETA: 0:00:00
Sampling  87%|████████████████████████████████████▌     |  ETA: 0:00:00

Sampling  88%|████████████████████████████████████▊     |  ETA: 0:00:00
Sampling  88%|█████████████████████████████████████     |  ETA: 0:00:00
Sampling  88%|█████████████████████████████████████▏    |  ETA: 0:00:00
Sampling  89%|█████████████████████████████████████▍    |  ETA: 0:00:00
Sampling  90%|█████████████████████████████████████▋    |  ETA: 0:00:00
Sampling  90%|█████████████████████████████████████▊    |  ETA: 0:00:00
Sampling  90%|██████████████████████████████████████    |  ETA: 0:00:00
Sampling  91%|██████████████████████████████████████▎   |  ETA: 0:00:00
Sampling  92%|██████████████████████████████████████▍   |  ETA: 0:00:00
Sampling  92%|██████████████████████████████████████▋   |  ETA: 0:00:00
Sampling  92%|██████████████████████████████████████▉   |  ETA: 0:00:00
Sampling  93%|███████████████████████████████████████   |  ETA: 0:00:00
Sampling  94%|███████████████████████████████████████▎  |  ETA: 0:00:00
Sampling  94%|███████████████████████████████████████▌  |  ETA: 0:00:00
Sampling  94%|███████████████████████████████████████▊  |  ETA: 0:00:00
Sampling  95%|███████████████████████████████████████▉  |  ETA: 0:00:00
Sampling  96%|████████████████████████████████████████▏ |  ETA: 0:00:00
Sampling  96%|████████████████████████████████████████▍ |  ETA: 0:00:00
Sampling  96%|████████████████████████████████████████▌ |  ETA: 0:00:00
Sampling  97%|████████████████████████████████████████▊ |  ETA: 0:00:00
Sampling  98%|█████████████████████████████████████████ |  ETA: 0:00:00
Sampling  98%|█████████████████████████████████████████▏|  ETA: 0:00:00
Sampling  98%|█████████████████████████████████████████▍|  ETA: 0:00:00
Sampling  99%|█████████████████████████████████████████▋|  ETA: 0:00:00
Sampling 100%|█████████████████████████████████████████▊|  ETA: 0:00:00
Sampling 100%|██████████████████████████████████████████| Time: 0:00:00

Sampling 100%|██████████████████████████████████████████| Time: 0:00:00

missing_data = similar(my_data, Missing) # vector of `missing`
model_missing = dice_throw(missing_data) # instantiate the "predictive model
prior_check = predict(model_missing, prior_chain);

typeof(prior_check)

Chains{Float64, AxisArrays.AxisArray{Float64, 3, Array{Float64, 3}, Tuple{AxisArrays.Axis{:iter, StepRange{Int64, Int64}}, AxisArrays.Axis{:var, Vector{Symbol}}, AxisArrays.Axis{:chain, UnitRange{Int64}}}}, Missing, NamedTuple{(:parameters, :internals), Tuple{Vector{Symbol}, Vector{Symbol}}}, NamedTuple{(), Tuple{}}}

summarystats(prior_check[:, 1:5, :]) # just the first 5 prior samples

Summary Statistics
  parameters      mean       std      mcse    ess_bulk   ess_tail      rhat    ⋯
      Symbol   Float64   Float64   Float64     Float64    Float64   Float64    ⋯
        y[1]    3.5300    1.7145    0.0444   1533.4233        NaN    1.0005    ⋯
        y[2]    3.5120    1.7371    0.0413   1758.6521        NaN    1.0006    ⋯
        y[3]    3.4985    1.7037    0.0402   1795.4112        NaN    1.0001    ⋯
        y[4]    3.4940    1.7031    0.0380   1974.3022        NaN    0.9996    ⋯
        y[5]    3.5285    1.7107    0.0388   1930.3860        NaN    0.9998    ⋯
                                                                1 column omitted