再入门基础

由于之前的python课没能将一些基础的操作学得透彻，只能再回炉重造一下。

包的引用

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels as sm

整数

conda install nb_conda ### 字符串

行话

由于你可能不太熟悉书中使用的一些有关编程和数据科学方面的常用术语，所以我在这里先给出其简单定义：

数据规整（Munge/Munging/Wrangling）指的是将非结构化和（或）散乱数据处理为结构化或整洁形式的整个过程。这几个词已经悄悄成为当今数据黑客们的行话了。Munge这个词跟Lunge押韵。

伪码（Pseudocode）算法或过程的“代码式”描述，而这些代码本身并不是实际有效的源代码。

语法糖（Syntactic sugar） 这是一种编程语法，它并不会带来新的特性，但却能使代码更易读、更易写。

import numpy as np
data = {i : np.random.randn() for i in range(7)}
data

{0: -0.6641839891537453,
 1: 0.5097008879665877,
 2: 0.6440338445822978,
 3: 0.5965156223580141,
 4: 0.23135186472436986,
 5: -0.2986398249522905,
 6: -0.09558735413887375}

通过输入代码并按下 return 运行任意Python语句。当只是输入一个变量，会显示代表的对象：

或者通过在chrome中输入法http://localhost:8888/ 手动打开notebook

自省

在变量前后使用问号，可以显示对象的信息：这可以作为对象的自省：若对象是一个函数或实例方法，定义过的文档都可显示出信息；

b=[1,2,3]
b?

`%run`命令

可以使用%run命令运行所有python程序。假设有一个文件：

def f(x, y, z):
    return (x + y) / z
a = 5
b = 6
c = 7.5
result = f(a, b, c)

#%run ipython_script_test.py即可实现

jupyter notebook 中的神奇命令

编辑模式（按esc进入）

Enter : 转入编辑模式

Shift-Enter : 运行本单元，选中下个单元

Ctrl-Enter : 运行本单元

Alt-Enter : 运行本单元，在其下插入新单元

Y : 单元转入代码状态

M :单元转入markdown状态

R : 单元转入raw状态

命令模式（按enter进入）

Tab : 代码补全或缩进

Shift-Tab : 提示

Ctrl-] : 缩进

Ctrl-[ : 解除缩进

Ctrl-A : 全选

Ctrl-Z : 复原

Ctrl-Shift-Z : 再做

Ctrl-Y : 再做

Ctrl-Home : 跳到单元开头

Ctrl-Up : 跳到单元开头

Ctrl-End : 跳到单元末尾

Ctrl-Down : 跳到单元末尾

Ctrl-Left : 跳到左边一个字首

Ctrl-Right : 跳到右边一个字首

Ctrl-Backspace : 删除前面一个字

Ctrl-Delete : 删除后面一个字

a=[1,2,3]
b=a
b

[1, 2, 3]

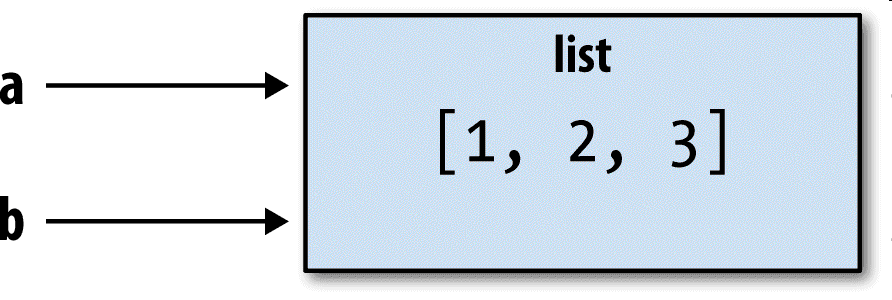
笔记：赋值也被称作绑定，我们是把一个名字绑定给一个对象。变量名有时可能被称为绑定变量。

python数据结构

程序的本质是针对数据的一种处理流程，有了不同的数据类型，程序才可以有的放矢的进行各种不同的数据操作。

数值型

常用的数值型包括int，float，comlex等。对于数值型的赋值和计算都较为直观。在python中，输入一个赋值语句就直接会将原有赋值清除。

x = 1
x = 5
print(x)

type(x)

int

a = b = c = 100 
print(a,b,c)

100 100 100

我们还可以对多个变量（对象）进行赋值。

bool类型数据

字符串类型

str1 = 'hello!\t this beautiful\t world!'
print(str1)

hello!   this beautiful  world!

使用\t来进行转义，还可以使用+或*来实现字符串的运算。

len(str1)

元组

元组与列表较为相似，可以用索引进行访问，可同样可以被嵌套，不同在于元组的元素一旦创建就不能再修改。有点像常量版本的列表。最为简单的创建方式——通过逗号隔开即可

tup1 = ()
type(tup1)

tuple

若元组只包含一个元素，则需要在元素之后添加逗号，代码如下：

tup1 = (100,)
type(tup1)

tuple

若不添加的话：

tup1 = (100)
type(tup1)

int

可以看见编译器对tup1作为一个整型对象，100的外围括号仅仅是一摆设。

因此可以更加简洁的实现生成一个元组，通过逗号进行分割即可实现。

a=1,2,3
a

tuple

用turble可以将任意序列转换为元组

tuple([4, 0, 2])
tup = tuple(['foo', [1, 2], True])
tup

('foo', [1, 2], True)

#连接元组
tup4 = ('Chinese',"chemistry",97,2.0)
id(tup4)

4699740816

因为元组的大小和内容不能修改，它的实例方法都很轻量。其中一个很有用的就是count（也适用于列表），它可以统计某个值得出现频率：

tup4

('Chinese', 'chemistry', 97, 2.0)

tup4 = tup4[:2]+("zhangsan",)+tup[2:]
id(tup4)

4699739616

tup4

('Chinese', 'chemistry', 'zhangsan', True)

在原先的元组进行插入之后，先通过分片技术，以第2个元素为基点，将原始元组拆分为两个部分，再中间插入一个。

对于不同元组的连接，通过加法操作符可完成。

tup.count([1,2])

列表

列表是python中最为常用的一个数据类型，与元组对比，列表的长度可变、内容可以被修改。你可以用方括号定义，不同的数据以逗号,分隔，或用list函数：

生成一个空列表

a = []
a

[]

a_list = [2, 3, 7, None]

a_list

[2, 3, 7, None]

append可以用于添加元素,insert可以用于在特定位置插入元素（在指定位置的末尾）

a_list.append(4)
a_list

[2, 3, 7, None, 4]

a_list.insert(1,10)
a_list

[2, 10, 3, 7, None, 4]

字典

dict1 = {key1: value1,key2:vaule2}

dict1 = {'a':1,'2020':[1,2,3],100:('hello','world')}

print(dict1)

{'a': 1, '2020': [1, 2, 3], 100: ('hello', 'world')}

删除的话使用pop

集合

集合和字典差不多

set([2, 2, 2, 1, 3, 3])

与字典类似，集合元素通常都是不可变的。要获得类似列表的元素，必须转换成元组：

my_data = [1, 2, 3, 4]
my_set = {tuple(my_data)}
my_set

NumPy

NumPy最重要的一个特点就是其支持N维数组对象（即ndarray），该对象是一个快速而灵活的大数据集容器。你可以利用这种数组对整块数据执行一些数学运算，其语法跟标量元素之间的运算一样。numpy的数组与列表有点相似，但仍然不同的是要纯洁一点，只能是一个数组类型。

import numpy as np

data = np.random.randn(2, 3)
data

data[1]

data[[1]]

因为data2是列表的列表，NumPy数组arr2的两个维度的shape是从data2引入的。可以用属性ndim和shape验证：

data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
arr2 = np.array(data2)

arr2.ndim

arr2.shape

np.zeros(10)
np.zeros((3,6))

每一个数组都有一个dtype属性，用于描述数组的数据类型。 np.array会自动推断数据类型。数据类型被存储在一个特殊的元数据dtype中。

import numpy as np
data1 = [6,8.5,9,0]
arr1 = np.array(data1)
arr1

arr1.dtype

arrage方法根据start与stop指定的范围及step设定的步长来生成一个ndarray对象，start为起时值。

arange(start,stop,step,dtype)

arange()根据start与stop指定的范围设定的步长范围，生成一个ndarray对象。

arr3 = np.arange(10)# generating 0-9 ndarray array
print(arr3)

print的时候的样子是不同于直接输出的

arr3

与range()函数较为相像，但range()生成的只能用于迭代。（属于一个迭代器）
np.range()的数据是左开右闭的，最后一个数取不到。当然可以在设置option中指定endpoint=False

np.ones_like(arr3)

np.empty_like(arr3)

import random
import matplotlib.pyplot as plt
position = 0
walk = [position]
steps = 1000
for i in range(steps):
    step = 1 if random.randint(0, 1) else -1
    position += step
    walk.append(position)

plt.plot(walk[:100])

import pandas as pd
import numpy as np

np.abs(-2)

基本控制流

grade = 95
if grade > 90:
    print('A')
else:
    if grade > 80:
        print('B')
    else:
        if grade > 70:
            print('C')
        else:
            if grade >60:
                print('D')
            else:
                print('F')

grade = 95
if grade > 90:
    print('A')
if grade > 80:
    print('B')
if grade > 70:
    print('C')

复杂数据结构

#### 1.5.1 list列表

l_1=[]
l_2=[1,2,0,'a','b',True]
print(l_1)
print(l_2)

ar1=np.array([0,1,2,3])
ar2=np.array([0,1,'2',3])
ar3=np.array([1.,2.,3.,4.])

ar1

ar2

print(ar3.dtype)

精度的不同，n.rate会进行转换，复杂性增大

全是浮点数，全让他为整型；仍然是向下取整
numpy的储存方式，是object对象，元素都是一个list

ts1 tensorflow 深度学习框架，推出一个以tensorprosing n层的数组，tensor一维是一个list，二维就是一个矩阵；这个方法就可生成

ar0=np.zeros(10,dtype=int)
ar1=np.empty(10)
ar2=np.ones((2,3),dtype=float)
ar3=np.full((2,3,3,),2.33)
ar4=np.indentity(5)#只要一个维度参数，生成单位矩

i1=np.eye(5)
i2=np.eye(5,7)
i3=np.eye(5,7,k=2)#k的值，表示值的移动方向

i1

i2

i3

#### 区间生成

ar5=np.arange(0,20,3)
ar6=np.linspace(10,30,7)#划分为7个区间

ar5

ar6

#### randomization

ar7=np.random.random((4,3))
ar8=np.random.normal(0,1,(4,4))
ar9=np.random.randint(0,9,(3,3))

ar7,ar8,ar9

np.random.seed(0)
ra1=np.random.random((3,4))
# real random and fake random(模拟出来的)seed is what we from
# seed(x),x is the number that random number is repitable 
# 在另外一行，连续的两个矩阵，是不同的；保证了代码的可复制性

数组属性

维度(dimension)都是由ndim属性来描述的。

ar1=np.ones((3,4,5))
print("the ar1's dim is",ar1.ndim,'\n',ar1.shape,'\n',ar1.size)
print(len(ar1))

print(ar2.dtype == ar3.dtype)

64bit 8byte\ 100M byte 10M bit

print(ar1.size)# 可以知道哪找bug

#function:astype
#ar1=ar1.astype(np.float)

对于N维数组而言，还有一个重要的属性是shape（数组形状），形状主要用于表征数组每个维度的数量，一维数组的形状就是它的长度一维也称为1D张量(1D tensor)

NumPy数组索引

ar1 = np.array([1,2,3,3])

ar1[1]

ar = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])

ar  #python的索引都是从(0,0)开始。

ar[0,2]

ar[0,:]#choose whole raw
# ‘：’将所有数选下来

ar[0]

#改数据类型必须符合原来的数据类型
ar[0,2]=5.14
ar

#切片/花式索引
ar[3::3] #第一个为开始，第二个为步长

ar[5:-1]

ar[:10:-2]

ar[:2,1:2]
#表示行全取

ar[::-1,::2]

ar[[0,1,2],[1,2,3]]
#按照对应索引来取之后仍然放在一个array之中

#[start=0:end=length:slice step]

ar,ar[1::],ar[1::2],ar[::2],ar[:1:]

取出一列，当最终出来的结果和一行类似；其实这本身就是函数的概念；

sub_ar=ar[1:,:2]
sub_ar

sub_ar_c=ar[1:,:2].copy() #father doesnot be effected

sub_ar

ar > 0 #return bool matrix

ar %2==0 #可将布尔值用于索引上

ar2=ar.reshape((1,12))
ar3=ar.reshape((12,1))

ar2,ar3

print(len(ar2))
print(len(ar1))

combination

ar_c1=np.concatenate([ar2,ar3.reshape(1,12)])

ar_c1

ll=list(range(10000))
%time ll=list(map(lambda x:x*2,ll))

map(lambda x:x*2,ll)

range(1000)

list(range(1,100))
 #range 到只有99

import numpy as np
ar = np.array(range(1,13)).reshape((3,4))

ar

(3,4)

ar*2

obj1=range(10)

obj1

obj1[9]

obj1?

timeit(obj1)

import random 
a=random.randint(0,100)
a

a*2

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.feature_selection import SelectKBest,f_regression
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor

boston_dataset=datasets.load_boston()
x_full=boston_dataset.data
y=boston_dataset.target
print(x_full.shape)
print(y.shape)

selector = SelectKBest(f_regression, k=1)
selector.fit(x_full,y)
X=x_full[:,selector.get_support()]
print(X.shape)

plt.scatter(X,y,color='black')
plt.show()

iris=datasets.load_iris()

print(iris.data)

import pandas as pd
import urllib2
url= "http://aima.cs.berkeley.edu/data/iris.csv"
set1=urllib2.Request(url)
iris_p=urllib2.urlopen(set1)

plt.scatter(X,y)
plt.show()

from sklearn.pipeline import make_pipeline

regressor=LinearRegression(normalize=True)#线性最小二乘估计来做，normalize
regressor.fit(X,y)
plt.scatter(X,y,color='black')
plt.plot(X,regressor.predict(X),color='blue',linewidth=3)
plt.show()

regressor=SVR() #SVR是指支持向量机的方式来实现
regressor.fit(X,y)
plt.scatter(X,y,color='black')
plt.scatter(X,regressor.predict(X),color='blue',linewidth=3)
plt.show()

随机森林

regressor=RandomForestRegressor()
regressor.fit(X,y)
plt.scatter(X,y,color='black')
plt.scatter(X,regressor.predict(X),color='blue',linewidth=2)

?RandomForestRegressor

A random forest is a meta estimator that fits a number of classifying decision trees on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting. The sub-sample size is controlled with the max_samples parameter if bootstrap=True (default), otherwise the whole dataset is used to build each tree.

type(regressor)

python中的函数

在python中的函数是以 def关键词定义开头，后接函数标识符号名称和圆括号()
传入参数必须放在圆括号之内，不同的参数用逗号隔开，即使没有参数，圆括号也需要保留
函数体以冒号开始，函数的作用范围需要统一缩进；
以return来结束函数，选择性的返回某个特定值给调用方。

def do_notiong():
    pass

函数返回多个值

def return_mul_val():
    my_str = "hello world"
    num = 20
    return my_str,num
str_, x = return_mul_val()
print(str_,x)

hello world 20

看上去好像是返回了多个值，但实际上只是一种假象，在python中，我们上述讨论到一个最为简易的生成元组的方式是通过逗号分隔数据，因此实际上上述的多个返回值本质上返回的是一个元组。

函数参数的花式传递

可变参数：在函数调用中，其参数并不固定，比如在使用C语言中，printf无论传递多少个参数都不会报错，在python中也可以较为方便的实现，在python中实现的方法是通过在形参前添加*，意味着函数传递的实参个数不定。而在函数内部，都被收集起来作为形参名为某个特定标识符的元组之中。

可变参数就可以被视为是“收集参数”

def mySum(*args):
    sum = 0
    for i in range(0,len(args)):
        sum = sum + args[i]
    return sum
print(mySum(1,2,3,4,5))
print(mySum(20.1,22.2))

15
42.3

另一种实现方法是通过两个星号**标识，将可变参数打包为字典形式。

数据改写

处理数据

利用numpy函数生成数组

需要由一个特定数字序列（0、1、序数和特定统计分布）组成的向量或矩阵，Numpy函数提供了很多的选择。

import numpy as np
ordinal_values = np.arange(9).reshape(3,3)#函数的一重重叠加
ordinal_values

np.arange(9)[::-1]

从列表到数组

list_of_ints=[1,2,3]
array_1=np.array(list_of_ints)
array_1

生成随机整数的数组（数组无序且可能重复），可以使用下面命令：

np.random.randint(low=1,high=10,size=(3,3)).reshape(3,3) #low和high确定的是上下界

np.zeros((3,3))

np.ones((3,3))

np.eye(3)

从pandas中提取数据（后面补充）

与pandas交互是可以很方便的，事实上，pandas是建立在Numpy上；

import pandas as pd
import numpy as np

Numpy数组的运算

list1 = [1,2,3,4,5,6,7,8,9]
list2 = [11,12,13,14,15,16,17,18,19]

list3 = [i+j for i in list1 for j in list2] #这个做法是错误的，只会形成两个嵌套循环，形成的数据维度就是1*（i*j）
list3 = [i+j for i,j in zip(list1,list2)] 
print(list3)

而对于numpy，先需要将列表转化为数组，而这个就直接可以用加号(+)

l1 = np.array(list1)
l2 = np.array(list2)
list_sum = l1+l2
print(list_sum)

算术运算

a = np.arange(5).reshape(1,5)

a+=1
a

a*a

还有很多的统计函数: - sum() - min() - max() - mean() - std()

同时还有一些数学函数: - sin() - cos()

逐元素运算与张量点乘运算

Numpy都是一个类矩阵的形式，因此NumPy中的数组在进行运算时候，都是基于基础算法库BLAS实现的。

a = np.array([[1,2],[3,4]])
a

a[0][0]#数组元素的提取,a[0]=array([1,2])，进一步提取a[0][0]=1

b = np.ones([2,2])
b

a + b

这时元素对元素原则，即数组的元素与元素位置对应相加。

数学意义上的矩阵乘法并非如此，不同形状的矩阵可以进行乘法运算。只要满足第一个矩阵的列与第二个矩阵的行数相同。

import numpy as np
a = np.arange(9).reshape(3,3)
a

b = np.ones(shape=(3,2))
b

np.dot(a,b) #a在前，b在后形成矩阵乘法。

转化为矩阵

a=np.mat(a)
a

b=np.mat(b)
b

np.mat() 将非矩阵的数据类型转换为矩阵输出

a*b  #satisfy multiplying directly

a = np.mat( np.random.random((3,3)) )  #(3,3) is the dimentions of data, always using tuple to describ
a  #we also use set.seed(n) to control the random rescult

a.I  #返回矩阵a的逆矩阵

a.T   #这些都是基于matrix的函数的一些操作

a.A  #返回对应的二维数组

广播机制(broadcasting)

a=np.arange(5).reshape(1,5)+1
b=np.arange(5).reshape(5,1)+1
a*b

#above is equviliant
a2=np.array([1,2,3,4,5]*5).reshape(5,5)
b2=a2.T
a2*b2

矩阵运算

M=np.arange(5*5,dtype=float).reshape(5,5)
M

coefs=np.array([1.,0.5,0.5,0.5,0.5])
coefs_matrix =np.column_stack((coefs,coefs[::-1]))
print(coefs_matrix)

np.dot(M,coefs)

np.dot(coefs,M)

np.dot(M,coefs_matrix)

爱因斯坦求和约定

einsum()不是一个简单的求和运算，而是一个高效的符号计算规则。

一个例子：点乘公式 $s = \sum_{i} v_{i} w_{i}$ 但小爱认为这个太繁琐，因此重新发明了一个符号计算公式： $s = v_{i} w^{i}$

仅仅用一个einsum()就可以实现求和、求外积、矩阵乘法等过程。 sum()和mat()以及trace()就会显得非常繁琐

einsum()理论上可支持任意多的参数。 - 不同的输入变量之间的格式要用逗号隔开； - 输入格式字符和输出格式字符要用箭头分隔开；

rescult = np.einsum('ijk,ijl->kl',a,b)

其中张量（数组）a就是一个三维矩阵，ijk是由三个字符构成，类似的输入张量b也是一个三维矩阵。

import numpy as np
arr = np.arange(10)
arr

sum1 = np.einsum('i->',arr)
sum1

einsum()通过求和，将一条线转化为一个点，也就是’i->’的含义。

arr2 = np.arange(20).reshape(4,5)
arr2
sum_col = np.einsum('ij->j',arr2)
sum_col

NumPy的轴方向

import numpy as np
a = np.ones((2,3))
a

a.sum()

元素的约简：实现在数量上的减少来反映数据，该原理同样适用于mean和max等

a.sum(axis = 1)

NumPy的高级索引

索引要么是一个，要么是一片值，自然只能访问一个数组元素。

花式索引是指将多个访问的元素索引汇集起来，构成一个整型数组，然后将这个内含索引的数组，整体作为一个目标数组的索引，一次能够读取多个重复的数组的元素。

normal_array = np.array([1,2,3,2,1,34,44,1,2])
normal_array

fancy_index_array = normal_array[[0,7,8,1]] #这样的形式可以提取多个
fancy_index_array

normal_array[[0,7,8,1]][1]

数组的堆叠操作

将不同的数组需要堆叠stack操作，拼接为一个较大的数组，堆叠方式大致可以分为水平方向堆叠和垂直方向堆叠。

数组NumPy的随机数

datascience process

EDA introduction

探索性科学(exploratory Data Analysis,EDA)是数据科学的第一步。EDA是John Tukey在1977年提出。

from sklearn import datasets
import numpy as np
import pandas as pd

iris=pd.read_csv('data/iris.csv',header=None,names=['sepal_length','sepal_width','petal_length','petal_width','target'])
iris.head()

iris.columns

取出数据列表中的一些东西

Y=iris.target
Y

异构列表

complex_list=[1,2,3]+[1.,2.,3.]+['a','b','c']
array_2=np.array(complex_list[:3])
print('complex_list[:3]',array_2.dtype)  #dtype=data_type
array_2=np.array(complex_list[:6])
print('complex_list[:6]',array_2.dtype)

iris.describe()

iris.boxplot()

df1=iris.quantile([0.1,0.9])
df1.to_csv(r"导出5.csv",index=False,header=True) #index和header默认为True

import os
print(os.path.abspath('.'))

use the data to plot

import matplotlib.pyplot as plt
plt.scatter(iris['petal_width'],iris['petal_length'],alpha=1.0,color='k')
plt.xlabel("petal width")
plt.ylabel("petal length")

plt.hist(iris.petal_width,bins=20)#bins是那分箱
plt.xlabel("petal width distribution")

分相值需要不断修正得到，一般来说是所有观测值的平方根。len(iris)=150 sqrt(150)=14

len(iris)

from sklearn import datasets
from sklearn.cross_validation import train_test_split
from sklearn.metrics import mean_squared_error
cali=datasets.california_housing.fetch_california_housing(
X=cali.data
y=cali.target
X_train,X_test,y_train,y_test=train_test_split(X,y,train_size=0.8))

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn import datasets

from sklearn import svm

维数化简

不得不将一些包含大量特征的数据集，其中有很多特征不必要的，有些特征包含丰富的信息，有些特征与预测相关。有些事完全不相关的。只是包含噪声或不相关信息。维数化简，消除输入数据集的某些特征。创建一个有限的特征数据集，这些特征包含所有需要的信息。从而更有效的预测目标变量。减少特征数意味着减少输出的变化性和复杂性（以及时间）。许多维数化简算法主要假设：数据包含加性高数白噪声（additive white gaussian Noise,AWGN),一种独立的高斯噪声。

协方差矩阵

协方差矩阵给出了所有不同的特征对之间的相关性。 Iris中有四个特征，通过简单的图形显示容易计算。

iris=datasets.load_iris()
cov_data=np.corrcoef(iris.data.T)#计算不同变量间的相关系数，以矩阵的形式表示。
print(iris.feature_names)

cov_data

import matplotlib.pyplot as plt
img=plt.matshow(cov_data,cmap=plt.cm.winter)
plt.colorbar(img,ticks=[-1,0,1])

主成分分析

主成分分析(principal component analysis,PCA)帮助于定义更小的、更相关特征集合的技术。新的特征就是现有特征的线性组合/旋转（按道理不算新特征）第二个向量与第一个向量正交，包含剩余能量的大部分。理想的加性高斯白噪声下。

from sklearn.decomposition import PCA
pca_2c=PCA(n_components=2)
x_pca_2c=pca_2c.fit_transform(iris.data)
x_pca_2c

plt.scatter(x_pca_2c[:,0],x_pca_2c[:,1], c=iris.target,alpha=0.8,edgecolors='none')
plt.show()

pca_2c=PCA(n_components=1,whiten=True)
x_pca_2c=pca_2c.fit_transform(iris.data)
plt.scatter(x_pca_2c[:,0],np.zeros(x_pca_2c.shape), c=iris.target,alpha=0.8,edgecolors='none')
plt.show()

2.2.3处理大数据集

要加载的数据集过大，而与采用的内存不适应，需要使用统一的机器学习方法。使用python可以加载数据到区块。该操作也称为数据流。数据集以连续流的形式流入数据框或其他的数据结构中。

3.3.3 一种用于大数据的PCA变型——Randomized PCA

PCA的主要问题在于它所采用的奇异值分解的复杂性。Scikit-learn提供了一种基于随机SVD(randomiezd SVD)的算法。另一方面，随机SVD比经典SVD更为快速。

from sklearn.decomposition import PCA as RandomizedPCA

rpca_2c=RandomizedPCA(n_components=2,svd_solver='randomized')
x_rpca_2c=rpca_2c.fit_transform(iris.data)
plt.scatter(x_rpca_2c[:,0],x_rpca_2c[:,1],c=iris.target,alpha=0.8,edgecolors='none')
plt.show()
rpca_2c.explained_variance_ratio_.sum()

目前来看的结果是与经典是接近的，但到大数据集中就显著会差异的。

3.3.4 潜在因素分析

LFA是另一种实现数据集降维分析的技术。总体思路与PCA方法相近。不需要度输入信号进行正交分解，因此没有输出基。 applied：主要在系统中有一个潜在因素或结构的情形。所有的特征是潜在因素经过线性变化后观测到的，具有任意波形发生器(AWG)的噪声。一般会认为，潜在因素符号高斯分布，具有归一化的协方差。

from sklearn.decomposition import FactorAnalysis
fact_2c=FactorAnalysis(n_components=2)
x_factor=fact_2c.fit_transform(iris.data)
plt.scatter(x_factor[:,0],x_factor[:,1],c=iris.target,alpha=0.8,edgecolors='none')
plt.show()

3.3.5 线性判别分析

LDA是一种分类器，经常用于维数约简。LDA是一种监督的方法。需要标签集来优化维数化简的步骤。LDA产生输入特征的线性组合，试图建立最能区分不同类别的模型与PCA相比，LDA方法获得的输出数据集能够清晰地分出各个类别。

3.4 异常检测和处理

样本是数据科学核心。变量中出现异常高的值，不仅会改变变量的均值和方差等描述性的测量还会影响到很多从数据中学习到的算法。从而使得这些算法暴露给异常值。数据点成为异常值的原因： - 数据点表示极少发生的事件，但仍然是一个可能的数据； - 数据点表示经常发生的另一种分布。 - 数据点明显是有某种类型的错误；

3.4.1 单变量异常检测

数据点的异常如何去说明，单变量的问题通常用EDA分析和箱线图等可视化方式实现。极端值可以被当作异常值。若使用z-scores，得分绝对值高于3的观测值必需当作可疑异常值。观测量是用数据描述

加载波士顿房价数据集，数据集中索引为3的变量CHAS是二进制（dummy variable）的，因此不使用该变量做。

import numpy as np
from sklearn.datasets import load_boston
boston = load_boston()
continuous_variables=[n for n in range(np.shape(boston.data)[1])if n!=3]
# 取出所有非3的变量

np.shape(boston.data)[1]
# shape use to check the dimention of array or matrix
# 1 means the column 0 means the rows

boston.data[1]

from sklearn import preprocessing 
normalized_data = preprocessing.StandardScaler().fit_transform(boston.data[:,continuous_variables])
outliers_rows,outliers_columns = np.where(np.abs(normalized_data)>3)
print (outliers_rows)

print(list(zip(outliers_rows,outliers_columns)))
# zip() 将对象压缩成一个新的元组。

由此，单变量方法可以检测出很多的异常值，但不能检测出那些不是极端值的异常值。若他可以发现两个或两个以上的变量组合出现非正常值。仍然会发现这个异常值。所涉及的变量可能不是极端值，因此这个异常值就可能会漏选。

3.4.2 EllipticEnvelope

EllipticEnvelope是用于找出数据总体分布的关键参数的函数。总体均值要考虑数据集中的所有变量。能够发现单变量和多变量的异常值。

3.4.3 oneclassSVM

EllipticEnvelope适用于有控制参数的高斯分布假设，而OneClassSVM适用于一种通过学习来得知分布。 - Kernel和Degree：这个两个变量是相关的。 - Gamma：是一个与rbf核相关的参数。 - nu ：是一个选择参数，决定模型是否必须符合一个精确的分布，还是应该尽量保持

3.5 评分函数

评估系统的性能并检查与目标距离，需要使用一个能对于结果进行评分的函数。通常有不同的评分函数分别处理二分类、多标号分类、回归或聚类问题。 #### 3.5.1多标号分类对一个进行预测时候，需要多标号分类。

from sklearn import datasets
iris = datasets.load_iris()
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,test_size=.50,random_state=4)
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(max_depth=2)
classifier.fit(x_train,y_train)
#用训练数据进行拟合
y_pred = classifier.predict(x_test)
#用测试数据做预测
iris.target_names

混淆矩阵(confusion matrix):又称可能性表格错误矩阵，其每一列代表预测值，每一行代表的是实际的类别。一个完美的分类，其混淆矩阵所有非对角线元素的都应0。

from sklearn import metrics
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test,y_pred)
print(cm)
print(y_pred)
print(y_test)

准确率(accuracy):准确率表示的是预测标号也是实际标号的比例。

print("Accuracy:",metrics.accuracy_score(y_test,y_pred))

二值分类

最常用的指标是ROC曲线或AUC曲线。ROC曲线是一种图形化方法，用于表示分类器性能是如何随可能的分类阀值改变的。

回归

MAE（L1 norm）mean_absolute_error

MSE（L2 norm）mean_squared_error

R2，决定了预测器与目标变量之间的线性拟合的好坏，取值在0-1之间。取值越高表示模型越好。sklearn.metrics.r2_score

交叉和验证

加载数据之后，经过预处理、创建新的特征、检查异常值和其他不一致的数据点等过程，完成了机器学习的算法准备。机器学习通过观测一系列样本，使样本与它们的结果相匹配，从而抽取一系列能够成功泛化到新样本的规则。一种有监督的学习方法。首先加载一个数据集：

from sklearn.datasets import load_digits
digits=load_digits()
print(digits.DESCR)
x=digits.data
y=digits.target
x
y

x[0]

from sklearn import svm
h1=svm.LinearSVC(C=1)#linear SVC means use the svm 
h2 = svm.SVC(kernel='rbf',degree=3,gamma=0.001,C=1.0)
h3=svm.SVC(kernel='poly',degree=3,gamma=0.001,C=1.0)

第一个实验我们对数据进行SVC拟合，并对结果进行检验。

h1.fit(x,y)
print(h1.score(x,y))

这个方法使用数组x拟合一个模型，以正确预测出向量中十个类别。然后调用.score()的方法，指定同一个预测器，用向量真值y进行评价模型性能。这个得分表示的是样本内(in-sample)性能，也是学习算法的性能。

交叉验证

当样本不同时候，验证和测试的结果也会有所不同；所选择的假设往往是最好的，但并非总是如此；可行方案：交叉验证。SL:sklearn.cross_validation

交叉验证，主要思想是在于将训练数据分为K组（折）训练模型k次，每次保留一个不同分组的不参与训练。十折是一个常见的设置。每次模型训练结束以后都会使用剩下的进行训练。标准差用于均值表示模型总体性能的公正估计。使用不同的模型交叉验证结果的均值。

from sklearn import cross_validation
choosen_random_state=1
cv_folds=10
eval_scoring='accuracy'
workers=-1
x_train,x_test,y_train,y_test=cross_validation.train_test_split(X,y,test_size=0.30,random_state=choosen_random_state)
for hypothesis in [h1,h2,h3]:
    scores = cross_validation.cross_val_score(hypothesis,x_train,y_train,cv=cv_folds,scoring=eval_scoring,n_jobs=workers)
    print("%s -> cross validation accuracy:mean =%0.3f std=%0.3f"%(hypothesis,np.mean(scores),np.std(scores)))

3.7.1 使用交叉验证迭代器

需要自己建立自己的交叉验证迭代器，cross_validation提供了一个较好的迭代器选择。 ##### KFold 折数n变量已知，根据训练集的索引进行n次迭代，每次都在剩下都验证集上测试。

kfolding = cross_validation.KFold(n=100,n_folds=10,shuffle=True,random_state=1)
for train_idx,validation_idx in kfolding:
    print(train_idx,validation_idx)

3.7.2 采样和自举方法

采样方法和之前的方法不同，不分割训练集，对训练集进行二次抽样(resample)或(mbootstrap) - 需要去选择一部分可以使用的数据，就需要二次抽样 - 二次抽样可以让你广泛的测试假设而又不用非常小的测试集中验证

from sklearn import model_selection
from sklearn import 
from sklearn.model_selection import train_test_split
subsampling = cross_validation.ShuffleSplit(n=100,n_iter=10,test_size=0.1,random_state=1)
for train_idx,validation_idx in subsampling:
    print(train_idx,validation_idx)

超参数优化

机器学习不仅取决于学习算法，还会受到超参数和变量选择的影响。其中超参数是算法事先确定的，无法在训练过程中学习得到。变量选择能够帮助假设获得最佳的参数。

Pandas

Series数据

Series数据是Pandas的核心数据结构之一。

Series创建

import pandas as pd
a = pd.Series([2,0,-4,12])
a

Series 的数据源用列表来填充，两者有相似之处，都是相同的类型，也可以是不同的类型。 series 增加对应的标签(label)作为索引，若没有，就默认是0～n-1内的索引值。

a.values

a.index

a.index=['a','b','c','d']
a

因为这种对应关系，因此对于Series可以使用字典的方式来实现对应的dict的key,series中的value相对应。

Dict = {'a':1,'b':2,'c':3,'d':4}

temp = pd.Series(Dict)
temp

Series中的数据是有序的，同时index和value是相互独立的，两者的索引也存在区别，Series和value是可变的。而字典的是不可变的。

temp.describe()

一些指标的含义： - count 一列数据的个数 - mean 一列数据的均值 - 25%:一列数据中前25的分位数

数据访问

可以通过特定索引值来访问、修改索引位置对应的数值，series对象再本质上就是一个带有Numpy数组，因此Numpy可直接运用于Series中。

cities = {"beijing":55000,"shanghai":40000,"shenzhen":10000,"hangzhou":20000,"guangzhou":30000}
apts = pd.Series(cities,name="prices")
apts

apts[0]

apts['beijing']

apts['beijing']=60000
apts

堆叠操作:append()

s1 = pd.Series([1,2,3])
s2 = pd.Series([2,3,4])

s1.append(s2,ignore_index=True)

Series中的向量化操作与布尔索引

apts*3

任何NaN(Not a Number)参与的计算，返回的结果依然是NaN。

向量化加法：

apts+apts

apts > apts.median()

会产生一个与原矩阵维度类似的bool矩阵。这个布尔矩阵也可以作为Series对象对应下标，用于获得值为True的位置的对应的数值。从而达到抽取特定样本的目的。

apts[apts > apts.median()]

切片操作

通过索引切片或处理Series中的一个或多个值，返回的结果依然是Series对象。

apts[1:3]

提取的是第一和第二个元素，第三个元素访问不到。

import numpy as np
arr = np.array([1,2,3,np.nan])
temp = pd.Series(arr,index=['a','b','c','d'])
temp

temp.isnull()

isnull()还可以把Series对象作为参数

pd.isnull(temp)

数据量庞大时候，缺失值可能处于正常数据中，这时候可以用布尔表达式形式，将这些数据筛选出来。

temp[temp.isnull()==True]

删除和添加

利用Pandas中的drop()

a = pd.Series([2,0,-4,12])
a

a.drop(0)  #这里的0指代原Series中的索引位置,而并非会影响原数据

a.drop([0,1])

print(a)

a.drop(0,inplace = True)

添加元素

a =pd.Series([1,2,3])

b =pd.Series(np.random.rand(3))  #np.random.rand(3) 生成0-1的随机数
b

a.append(b)

a.append(b,ignore_index=True)

DataFrame

若将Series看作Excel的一列，则DataFrame就是一张表

import numpy as np
import pandas as pd
data1 = np.random.randint(1,10,9).reshape(3,3)

data1

np.random.randint(1,9)  #生成在1-9的整数随机数

df1 = pd.DataFrame(data1)
df1

改变index行名，显示指定列名

df2 = pd.DataFrame(data1,columns=['one','two','three'],index=['a','b','c'])
df2

df2.T

访问DataFrame中的列和行

df2.columns

df2.columns.values

在pandas，Dataframe可以将列的名称作为DataFrame对象的属性来访问数据。

df2.one

df2['one']

上述两者是等价的

DataFrame中的删除操作

类似于Series，可以同样使用drop来删除一行或一列

Dataframe的轴方向

基于Pandas的文件读取与分析

Matplotlib 与Seaborn可视化分析

Matplotlib与图形绘制

matpltlib.pyplot.figure
(
    num = None,       # 设定figure名称。系统默认按数字升序命名的figure_num（透视表输出窗口）e.g. “figure1”。可自行设定figure名称，名称或是INT，或是str类型；
    figsize=None,     # 设定figure尺寸。系统默认命令是rcParams["figure.fig.size"] = [6.4, 4.8]，即figure长宽为6.4 * 4.8；
    dpi=None,         # 设定figure像素密度。系统默命令是rcParams["sigure.dpi"] = 100；
    facecolor=None,   # 设定figure背景色。系统默认命令是rcParams["figure.facecolor"] = 'w'，即白色white；
    edgecolor=None, frameon=True,    # 设定要不要绘制轮廓&轮廓颜色。系统默认绘制轮廓，轮廓染色rcParams["figure.edgecolor"]='w',即白色white；
    FigureClass=<class 'matplotlib.figure.Figure'>,   # 设定使不使用一个figure模板。系统默认不使用；
    clear=False,                     # 设定当同名figure存在时，是否替换它。系统默认False，即不替换。
    **kwargs
)

import math
import numpy as np
import matplotlib.pyplot as plt

nbsample = 256
xrange = [-math.pi,math.pi]
x ,y = [],[] #create the void list
for i in range(nbsample):
    ratio = (i + 0.5)/nbsample
    x.append(xrange[0]+(xrange[1]-xrange[0])*ratio)
    y.append(math.sin(x[-1]))  #反向操作，将列表中的最后一个元素带入函数，再append in y

plt.plot(x,y)
plt.show()

上述做法可以用numpy来得到简化

x = np.linspace(-math.pi,math.pi,num=256)
y=np.sin(x)
plt.plot(x,y)
plt.show()

linspace(linspace(start,stop,num=50))能够批量生产指定区间内的数量为num的均匀间隔的数组向量。

import numpy as np
import matplotlib.pyplot as plt
nbsample = 128

x = np.linspace(-np.pi,np.pi,nbsample)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x,y1,color='g',linewidth=4,linestyle='--')
plt.plot(x,y2,markersize=9,markerfacecolor='r',markeredgecolor='k')

`pyplot`的高级功能

添加图例和注释

import numpy as np
import matplotlib.pyplot as plt
nbsample = 128

x = np.linspace(-np.pi,np.pi,nbsample)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x,y1,color='g',linewidth=4,linestyle='--')
plt.plot(x,y2,markersize=9,markerfacecolor='r',markeredgecolor='k')
plt.legend("loc=best")
plt.show()

设置图形标题及坐标轴

import numpy as np
import matplotlib.pyplot as plt
nbsample = 128

x = np.linspace(-np.pi,np.pi,nbsample)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x,y1,color='g',linewidth=4,linestyle='--')
plt.plot(x,y2,markersize=9,markerfacecolor='r',markeredgecolor='k')
plt.title("tangle function plot")
plt.xlabel("x")
plt.ylabel("y")
plt.show()

添加网格线

使用plt.grid()即可实现。

data = np.arange(0,4,0.2)
plt.plot(data,data,'r-.',data,data**2,'bs',data,data**3,'g^')
plt.grid(b=True)
plt.savefig('mult_lines-grid.png',dpi=600)

/var/folders/sn/g01cvq2j72j6tbq2pmmm074h0000gq/T/ipykernel_44709/2338610709.py:4: MatplotlibDeprecationWarning: The 'b' parameter of grid() has been renamed 'visible' since Matplotlib 3.5; support for the old name will be dropped two minor releases later.
  plt.grid(b=True)

绘制多个子图

实际上有时候需要多个子图，使用subplot()

def f(t):
    return np.exp(-t) * np.cos(2 * np.pi * t)

t1 = np.arange(0,5,0.01)
t2 = np.arange(0,5,0.02)
plt.figure(12)
plt.subplot(221)
plt.plot(t1, f(t1), 'bo', t2, f(t2), 'r--')
plt.subplot(222)
plt.plot(t2, np.cos(2 * np.pi * t2), 'r--')
plt.subplot(212)
plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.show()

整个图形按照2*2进行划分，前两为(2,2,1)和(2,2,2)，第三个图直接占据的是第三块和第四块，按照2*1来划分，因此，前两张图合并为(2,1,1)后一张为(2,1,2)

from random import uniform
from scipy.stats import norm

num_rows, num_cols = 3, 2
fig, axes = plt.subplots(num_rows, num_cols)
for i in range(num_rows):
    for j in range(num_cols):
        m, s = uniform(-1, 1), uniform(1, 2)
        x = norm.rvs(loc=m, scale=s, size=100)
        axes[i, j].hist(x, alpha=0.6, bins=20)
        t = f'$\mu = {m:.2}, \quad \sigma = {s:.2}$'
        axes[i, j].set(title=t, xticks=[-4, 0, 4], yticks=[])

plt.tight_layout()
plt.show()

散点图

import numpy as np
import matplotlib.pyplot as plt
nbpoint=50
np.random.seed(100)
x = np.random.standard_normal(nbpoint)
x

y = np.random.standard_normal(nbpoint)
np.random.seed(1000)
colors = np.random.rand(nbpoint)
area = (30*np.random.rand(nbpoint))**2
plt.scatter(x,y,s=area,c=colors,alpha=0.3)
plt.show()

其中参数alpha表示透明度，s就是plot()中的markersize参数。

条形图和直方图

并列条形图

叠加条形图

直方图

饼图

箱形图

误差条

绘制三维图形

matplotlib对三维图形的支持很强大：

from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm

def f(x, y):
    return np.cos(x**2 + y**2) / (1 + x**2 + y**2)

xgrid = np.linspace(-3, 3, 50)
ygrid = xgrid
x, y = np.meshgrid(xgrid, ygrid)

np.meshgrid生成的是网点坐标，也就是将二维的数据传递进去，生成出三维的数据矩阵。

主要使用的函数是plot_surface，传入参数为x，y和一个z=f(x,y)三个坐标轴。

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x,
                y,
                f(x, y),
                rstride=2, cstride=2,
                cmap=cm.jet,
                alpha=0.7,
                linewidth=0.25)
ax.set_zlim(-0.5, 1.0)
plt.show()

惊艳的Seaborn

Seaborn基于Matplotlib的数据可视化库，在Matplotlib的基础上实现了一些好用的功能，在代码形式上会更加像R语言上的ggplot。

Scipy

np.random.beta(5, 5, size=3)

array([0.24123322, 0.31978638, 0.54168125])

This generates a draw from the distribution with the density function below when a, b = 5, 5

$f (x; a, b) = \frac{x^{(a - 1)} (1 - x)^{(b - 1)}}{\int_{0}^{1} u^{(a - 1)} (1 - u)^{(b - 1)} d u} (0 \leq x \leq 1)$

但一些时候我们需要生成的是密度，或者cdf，或分位数等。因此可以使用scipy.stats来实现

from scipy.stats import beta
import matplotlib.pyplot as plt
%matplotlib inline

q = beta(5, 5)      # Beta(a, b), with a = b = 5
obs = q.rvs(2000)   # 2000 observations
grid = np.linspace(0.01, 0.99, 100)

fig, ax = plt.subplots()
ax.hist(obs, bins=40, density=True)
ax.plot(grid, q.pdf(grid), 'k-', linewidth=2)
plt.show()

q.cdf(0.4)  # Cumulative distribution function

0.26656768000000003

q.ppf(0.8)

0.6339134834642708

q.mean()

0.5

import quantecon as qe

OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.

α = 4.0

def qm(x0, n):
    x = np.empty(n+1)
    x[0] = x0 
    for t in range(n):
      x[t+1] = α * x[t] * (1 - x[t])
    return x

x = qm(0.1, 250)
fig, ax = plt.subplots()
ax.plot(x, 'b-', lw=2, alpha=0.8)
ax.set_xlabel('$t$', fontsize=12)
ax.set_ylabel('$x_{t}$', fontsize = 12)
plt.show()

from numba import jit

qm_numba = jit(qm)

n = 10_000_000

qe.tic()
qm(0.1, int(n))
time1 = qe.toc()

TOC: Elapsed: 0:00:5.39